Methode zur Generierung selbstorganisierender Prozesse für
            autonome Mechanismen und Organismen

Verstreichzeit-Quantifizierung Autoadaptions-Theorem Algorithmus des Lebens Der neuronale Code Die Bedeutung des Tetragrammatons "JHWH" Ein Schritt zu einer neuen Universal-Theorie? Patent & Patentschriften: US     US 6172941 (eingereicht 16 12 1999) EP     EP 01145406 A1 (eingereicht 03 12 1999) Österreich: Nr. A 767/2000  (eingereicht 28 04 2000) Erfinder & Autor: Erich Bieramperl, 4040 Linz, Österreich

Lesen Sie auch: Die Dokumentation über den größten                       vorstellbaren Patent- und Erfinderskandal:                       Alles über  SENSOR TIMING / 1978 bis 2010

             Abstract

Die Erfindung beschreibt eine Methode zur Generierung von Auto-Adaption und Selbstorganisation in autonomen Einheiten, z.B. Mechanismen und Organismen, bei denen eine Vielzahl von Sensoren angeordnet ist, die in verschiedene Wahrnehmungs-Bereichszonen unterteilt sind. Die zeitlich/räumlichen Zustands- veränderungen zwischen den Einheiten und ihrer physikalischen Umgebung produzieren Signalamplituden, wobei die aktuellen Verstreichzeiten zwischen den Phasendurchgängen proportional zur jeweiligen Relativgeschwindigkeit quantisiert, registriert, und fortgesetzt mit früheren Verstreichzeiten verglichen werden. Aus entdeckten kovarianten Zeitsequenzen und Zeitmustern erkennt der Mechanismus oder Organismus seinen eigenen Bewegungsverlauf und kann mittels kovarianzgeregelten Energieimpulsen dazu verhalten werden, stets jenen Zustandsveränderungen nachzueifern, für welche die entdeckten kovarianten Zeitsequenzen und Zeitmuster signifikant sind.

	Background
		Die Erfindung beschreibt eine Methode zur Generierung selbstorganisierender Prozesse für Prozesse für autonome Systeme. Sie erstreckt sich sowohl auf den artifiziellen mechanistischen Bereich als auch auf Systeme molekular/ biologischer und anderer Art. Mittels der beschriebenen Erfindung ist es möglich, externe Ereignisse mit variablem Bewegungsverlauf aus subjektiver Sicht des Systems in Echtzeit zu identifizieren, Zustandsveränderungen zu erkennen, Eigenbewegungen nachzuvollziehen und zu optimieren, sowie redundanzarme Prozesse zur Selbst- organisation herzuleiten. Robotik-Systeme der üblichen stationären Art stützen sich hauptsächlich auf deterministische weg-abhängige Regelungs- oder Steuerungsprozesse. Die Regelgrößen oder Stellwerte zu jeder Position sind zumeist im Programmspeicher eines Computers enthalten. Durch Anordnung mehrerer Wegbezugsebenen können verschiedene Freiheitsgrade festgelegt werden. Als Wegaufnehmer dienen Tacho- Geber, Encoder oder Strichcode-Lineale, die von optischen Sensoren abgetastet werden und Wegstrecken-Zählimpulse liefern. Der Antrieb erfolgt zumeist mittels Schrittmotore. Es ist auch bekannt, in wegabhängigen Programmsteuerungen zusätzliche adaptive Regelungsprozesse vorzusehen, welche auf Daten basieren, die nach der SHANNON- Quantisierungsmethode (auch "Sampling" genannt) aus den Amplituden von Sensor- bzw. Messfühler- Signalen gewonnen werden. Sie dienen zur Korrektur und Modifikation des Ist-Zustandes. Ein fortgesetzter Vergleich von Soll- und Istwerten ist erforderlich zur Korrektur und Modifikation des Regelungs-Prozesses. Die errechneten neuen Regel-Parameter werden dann in den Programmspeicher übernommen. Diese Art von adaptiven Regelungen ist beispielsweise notwendig, um bei einem Handhabungs-Roboter Abweichungen vom festgelegten Bewegungsverlauf auszugleichen, der durch unterschiedliche Lastzustände entsteht. Wenn ein Roboter oder ein roboter- gesteuertes Vehikel in dieser Weise in einen autonomen Status versetzt werden soll, so ist es aber in den meisten Fällen unmöglich, die genaue Position (oder Koordinaten) durch Tacho- oder Encoderimpulse zu bestimmen. Regelgrößen oder Steuerbefehle können daher nicht exakt vom Computer ausgegeben bzw. im Rechner vorprogrammiert werden. Dies betrifft nicht nur roboter- gesteuerte Autos, gleitende Vehikel, Hovercrafts oder Flugzeuge aller Art, sondern auch schienengebundene Fahrzeuge, wo die Ableitung von Wegstrecken- Zählimpulsen oftmals ungenau und nicht reproduzierfähig ist. Verursacht wird dies durch Unebenheiten, Radschlupf oder Radabnützung. Erkundungs- oder Handhabungsroboter, die etwa zur Ortung oder Bergung von Gegenständen an schwer zugänglichen oder gefährlichen Stellen eingesetzt werden, müssen daher manuell oder mit Computer-Unterstützung ferngesteuert werden. In solchen Fällen sind Daten- oder Bildübertragungssysteme erforderlich, um auf einem Monitor die Bewegungsvorgänge des Roboters überwachen zu können. Bei vielen Roboter- Anwendungen ist dies jedoch nicht sinnvoll. Ein roboter-gesteuertes Automobil sollte beispielsweise imstande sein, ohne menschliche Intervention Objekte in Echtzeit zu erkennen, Gefahrensituationen auszuweichen und seine Geschwindigkeit an die Umweltsituation anzupassen. In solchen Fällen ist es notwendig, dass der Bordcomputer die Situation vor Ort erkennen und die auszuführenden Schritte errechnen kann. Somit sollte das roboter-gesteuerte Vehikel über ein gewisses Maß an Fähigkeit zur Selbstorganisation verfügen. Dieselben Erfordernisse gelten auch für andere Robotik-Systeme. Zwar ist es in bezug auf autonome mobile Robotersysteme auch bekannt, das ambiente Umfeld mittels Sensoren abzutasten und die durch zeitdiskrete Quantisierung (s. Fig. 1) erhaltenen digitalen Sampling- Daten im Bordcomputer zu analysieren; und es existieren auch statistische Rechenverfahren und Algorithmen, um die entsprechenden Regelparameter bereitzustellen. Statistische Methoden zur Abwicklung solcher Regelsysteme wurden bereits 1949 von Norbert WIENER beschrieben. Nach dem bekannten SHANNON-Theorem hat hierbei die Abtastung des Umfeldes mit mindestens der zweifachen Frequenz der Signalamplituden-Bandbreite zu erfolgen. Damit bleibt ihr Informationsbetrag erhalten. Um die Eigenbewegung erfassen zu können, sind sehr hohe Abtastraten erforderlich. Diese weit verbreitete Amplituden-Quantisierungsmethode erfordert die Korrelation erfasster Messdaten zu jeweiligen vom Program Counter fix vorgegebenen Zeitpunkten (Ts). Demnach kann dies als deterministischer Prozess verstanden werden. Die Praxis hat jedoch gezeigt, dass selbst bei Verwendung sehr schneller Prozessoren und höchster Samplingraten keine ausreichende Effizienz erreicht werden kann. Die Zahl redundanter Daten und Rechenoperationen steigt drastisch an, wenn ein sensorgesteuertes Vehikel auf neue Hindernisse trifft oder sich mit variabler Geschwindigkeit auf neue Umwelt- Gegebenheiten adaptieren soll. Tatsächlich lässt Claude Shannons Quantisierungsmethode keine Erkennung eines analogen Signalamplituden-Verlaufes in Echtzeit zu; insbes. bei wechselnden physikalischen Zuständen oder variablen Bewegungsverläufen, welche die Erfassung zusätzlicher Information über die Momentan-Geschwindigkeit erforderlich macht. Dies gilt grundsätzlich auch bei Verwendung von Laser- oder Ultraschallsensoren, bei denen Entfernungsdaten digital erfasst und verarbeitet werden. Daher eignet sich diese Quantisierungsmethode zwar dazu, den Spurverlauf einer Eigenbewegung zu rekonstruieren, wie dies in Pat. AT 397 869 beschrieben ist, jedoch kaum zur Erkennung der Eigenbewegung des Roboters oder zu deren auto-adaptiven Reproduzierung. Manche autonome mobile Robotersysteme arbeiten mit CCD- Kameras und OCR-Software (Bildanalyse-Verfahren). Sie schließen aus Farbkontrasten und Helligkeitsunterschieden auf Konturen oder Objekte, die vom Computer als anzusteuernde Ziele oder als Orientierungs- Merkmale interpretiert werden. Beispiele dafür sind rechnergestützte Leit- und Lenksysteme, welche die automatische Nachführung von Fahrzeugen durch Mittellinien, Seitenplanken oder Straßenränder ermöglichen. CCD- Sensoren sind - wenn man ihre Arbeitsweise betrachtet - Analogspeicher, die nach dem bekannten Eimerkettenprinzip funktionieren. Auf einem MOS- Siliziumchip befinden sich dichtgepackte Kondensatoren, die durch den fotoelektrischen Effekt auf ein bestimmtes Potential aufgeladen werden. Jedes Ladungspaket entspricht einem bestimmten Bildpunkt, genannt "Pixel", wobei die Ladung jedes Pixels Aufschluss über die Helligkeit an der jeweiligen Stelle des Bildes gibt. Durch Anlegen von Steuerspannungs- Frequenz werden die Ladungspakete Pixel für Pixel über das CCD verschoben, wo sie am Output als serielle Videosignale erscheinen. Um sie im Computer zu verarbeiten, müssen sie in digitale Größen umgewandelt werden. Ihre Verarbeitung erfordert eine hohe Anzahl von redundanten Daten und Rechenprozessen, weshalb die digitale Erfassung von längeren Sequenzen elektronische Speicher mit extrem großer Kapazität erfordert. Eine Erkennung isomorpher Sequenzen in Bewegungsverläufen ist nur mit großem Aufwand und in zeitlicher Versetzung möglich, weshalb derartige auf CCD- Sensoren basierende Robotiksysteme nur in sehr beschränkter Weise zur auto-adaptiven Nachvollziehung von Eigenbewegungen geeignet sind. Bei jeder Wiederholung desselben Bewegungsvorganges an gleicher Strecke müssen alle Regelparameter mittels Bildanalyse neu berechnet werden. Verändern sich Umweltbedingungen durch Nebel, Dunkelheit oder Schneefall, sind solche Systeme zumeist überfordert und nicht einsetzbar. Pat. AT 400 028 beschreibt ein System zur adaptiven Regelung eines motorgetriebenen Vehikels, wobei Markierungen oder Signalquellen entlang der Strecke angeordnet sind, um als Wegweiser zur Einhaltung eines Fahrplanes zu dienen. Auch Positionen, die durch GPS- Signale ermittelt werden, können dazu dienen. Beim Passieren dieser Quellen misst das bordseitige sensor-gekoppelte Computersystem die benötigten Zeiten für jeden zurückgelegten Streckenabschnitt mittels der in Pat. U.S. 4,245.334 beschriebenen Weise der Zeitquantisierung durch erste und zweite Sensorsignale. Die auf diese Art erworbenen Daten dienen als Referenzbasis für die Errechnung jener Regelparameter, welche die Antriebs- und Bremszyklen des Vehikels steuern. Das System arbeitet mit einer geringen Zahl redundanter Daten, korrigiert sich in auto-adaptiver Weise selbst, und ist imstande, eine elektronische "Marschtabelle" nachzuvollziehen. Es eignet sich insbes. zur Einhaltung von Streckenfahrplänen im Schienenverkehr. Allerdings ist es mit diesem System nicht möglich, ambiente Objekte Umgebungen festzustellen. Es ist Aufgabe dieser Erfindung, eine umfassende Methode zur Generierung autonomer selbst-organisierender Robotik-Systeme bereitzustellen, die es ermöglicht, externe Signale, Objekte, Ereignisse, physikalische Zustände oder Umgebungen aus subjektiver Sicht in Echtzeit zu identifizieren. Dadurch wird es ermöglicht, die Muster von Eigenbewegungen zu erkennen und die eigene Verhaltensweise in autoadaptiver Weise zu reproduzieren und zu optimieren. Es ist eine weitere Aufgabe der Erfindung, mittels dieser Methode einen autonomen Trainingsroboter für den Einsatz im Sport bereitzustellen, der imstande ist, einen vom Benutzer vorgegebenen Bewegungsverlauf zu identifizieren, zu reproduzieren und zu optimieren; außerdem die ideale Spur und Tempoverteilung selbsttätig zu suchen, bestimmte Abstände und Zeittabellen einzuhalten, Eigenbewegungs-Verläufe, Geschwindigkeiten, Rundenzeiten, Teilzeiten und Gesamtzeiten auf einem Monitor darzustellen; sowie die erfassten Daten optisch oder akustisch auszugeben.

	Zusammenfassung der Erfindung
		Die gestellten Aufgaben werden bei der erfindungsgemäßen Methode im Allgemeinen durch Anordnung von Sensoren oder Rezeptoren an dem sich bewegenden System (z.B. einem autonomen Robotik-System) gelöst, welche die ambienten Signalquellen, deren Amplituden durch Festlegen einer Anzahl von Schwellwerten unterteilt werden, abtasten. Dadurch werden Wahrnehmungsbereichszonen geschaffen. Die Verstreichzeiten aller Phasendurchgänge in allen Zonen werden mittels analoger oder digitaler STQ-Quantisierung fortgesetzt erfasst, und die Zeitzähltakte in Abhängigkeit von der relativen Momentan- Geschwindigkeit, die durch die Phasenverschiebung der Signalverläufe benachbarter gleichartiger Sensoren bestimmt ist, automatisch moduliert. Die gezählten Impulse korrelieren annähernd mit den zurückgelegten Distanzwerten (dnnn). Bei dieser Methode ist die Abtastung von Signalamplituden kein deterministischer Prozess; sie erfolgt nicht zu vorgegebenen Zeitpunkten in bestimmten Zeittakten. Die Erfassung, Verarbeitung und Analyse der Verstreichzeiten erfolgt weitgehend nach probabilistischen Prinzipien. Daraus resultiert die physikalisch bedeutsame Tatsache, dass die Parameter zur Beschreibung der externen Umgebung vom System eigentlich nicht "objektiv gemessen", sondern als zeitliche Abfolgen quasi "subjektiv empfunden" werden. Das System selbst fungiert hierbei als "Beobachter" des Prozesses. In der technischen Fachliteratur werden Verstreichzeiten (im Zusammenhang mit deterministischem Timing) auch als "Signal- Laufzeiten" oder "Zeitintervalle" bezeichnet. Bei der beschriebenen Erfindung erfolgt die Quantisierung der sogenannten "STQ-Verstreichzeiten" im Verlauf des Signalerkennungs- Prozesses durch Starten und Stoppen einer Vielzahl von Zeitmessern an allen Phasen- Übergängen. Sie ergeben zusammen einen Strom von Zeitdaten. Jede Verstreichzeit zwischen Phasendurchgängen in der gleichen Wahrnehmungsbereichszone kann ebenso erfasst werden wie die Verstreichzeiten zwischen den Phasendurchgängen von einem niedrigen zu einem höheren Schwellwert und umgekehrt. Man unterscheidet grundsätzlich drei verschiedene Arten von STQ-Quantisierung (bzw. Verstreichzeitmessung):   STQ(v) = sensitive time quantum - velocity = Tv1,2,3... ....ist die Verstreichzeit, festgelegt durch die beim Vorbeibewegen eines ersten Sensors bzw. Rezeptors S2 und eines gleichgearteten zweiten Sensors bzw. Rezeptors S entlang einer korrespondierenden externen Signalquelle Q hervorgerufene Signal- amplitude. Sie wird von der steigenden Flanke beim Phasendurchgang iTv1.1 des ersten Sensorsignals zur steigenden Flanke beim Phasendurchgang iTw1.1 des zweiten Sensorsignals, desgl. von iTv2.1 zu iTw2.1, von iTv3.1 zu iTw3.1 usw. gemessen., wobei sich die Phasendurchgänge auf die gleichen Schwellwertpotentiale P1,2,3... beziehen. STQ(v)- Zeiten können auch von fallenden Flanken gemessen werden. Sie dienen als Parameter für die momentane Relativgeschwindigkeit (vm) des sich bewegenden Systems.   STQ(i) = sensitivity/time quantum of interarrival = Tw1,2,3... ....ist die Verstreichzeit, festgelegt durch die von einem Sensor (bzw. Rezeptor) S1 im Feld einer korrespondierenden externen Signalquelle Q und/oder durch die beim Vorbeibewegen eines Sensors bzw. Rezeptors S entlang mehrerer gleichartiger externer Signalquellen Q1,2,3...hervorgerufene Signalamplitude. Die Verstreichzeit wird gemessen von der steigenden Flanke beim Phasendurchgang iTw1.1 des steigenden Sensorsignals zur fallenden Flanke beim Phasendurchgang iTw1.2 des fallenden Sensorsignals, desgl. von iTw2.1 zu iTw2.2, von iTw3.1 zu iTw3.2 usw., sowie von der fallenden Flanke beim Phasendurchgang iTw1.2 weiter zur nächsten steigenden Flanke beim Phasendurchgang iTw1.3, desgl. von iTw2.2 zu iTw2.3, von iTw3.2 zu iTw3.3 usw., wobei sich die Phasendurchgänge auf die gleichen Schwellwert- potentiale P1,2,3....beziehen. Wird die Zeitzählfrequenz für die Messung der STQ(i)- Verstreichzeiten Tw(1,2,3...) proportional zur momentanen Relativgeschwindigkeit vm (welche mittels STQ(v)- Parameter erfasst ist) erhöht oder verringert, so haben die gezählten Impulse korrelativen Bezug zur Strecke, die das sensor-gekoppelte System zurückgelegt. Es ist klar ersichtlich, dass die solchermaßen adaptierten Verstreichzeiten nicht ident mit realen physischen Zeiten sind, die von üblichen Zeitmessern für jene relative Strecke gemessen würden. Besteht jedoch absolute physikalische Invarianz zwischen dem sich bewegenden System und seiner Umgebung (z. B. Synchronität), so kann kein STQ-Parameter erfasst werden.   STQ(d) = sensitivity/time quantum of differentiation = Td1,2,3... ....ist die Verstreichzeit, festgelegt durch die von einem Sensor (bzw. Rezeptor) S1 im Bereich einer korrespondierenden externen Signalquelle Q1,2,3.. hervorgerufene Signalamplitude, gemessen von der steigenden Flanke beim Phasendurchgang iTw1 des steigenden Sensor-Signalverlaufes zur steigenden Flanke beim nächsthöheren Phasen- Durchgang iTw2, von iTw2 zu iTw3, von iTw3 zu iTw4 usw., sowie in umgekehrter Folge beim fallenden Signalverlauf, wobei sich die Phasendurchgänge auf die gleichen Schwellwertpotentiale P1,2,3..beziehen. STQ(d)-Daten stellen Differential- Parameter für die Flankensteilheit von Signalamplituden dar und somit für deren Frequenz, außerdem dienen sie der Plausibilitätsprüfung und Verifizierung von anderen korrespondierenden STQ- Verstreichzeitdaten. Die Relativbewegung zwischen Sensor und Signalquelle wird bei dieser Messung nicht berücksichtigt. Besteht keine Relativbewegung zwischen Sensoren und Quellen (jedoch Varianz von Feldern) so werden Zustandsveränderungen eines Feldes aus STQ(i)- und STQ(d)- Verstreichzeiten erfaßt und identifiziert. Wenn aber absolute physikalische Invarianz gegeben ist, können keine STQ- Quanten erfasst werden, und Erkennung ist ausgeschlossen. STQ(v)- Daten werden vorwiegend dazu benötigt, um die räumliche Umgebung unter relativer Bewegung erkennen und/oder aus identifizierten Bewegungsprozessen die eigene Bewegung (oder Teile dieser Bewegung) erkennen sowie in auto-adaptiver Weise nachvollziehen zu können. Bei einer im mechanistischen Bereich angewandten Ausführungsform der erfindungsgemäßen Methode werden die genannten Wahrnehmungsbereichszonen üblicherweise durch eine Anzahl elektronischer Schwellwertdetektoren mit unterschiedlich eingestellten Empfindlichkeitspegel gebildet, und die STQ(i)- und STQ(d)- Verstreichzeitdaten werden mittels programmierbarer digitaler Timer erfasst. Der Verstreichzeit- Registrierungsprozess wird an einem iT- Phasendurchgang sowohl gestartet als auch gestoppt. Dann wird die Zeitdate in einem Memory gespeichert. Ferner können besagte STQ(v)- Verstreichzeiten mittels elektronischer Integratoren erfasst werden, wobei die Aufladezeiten der Kondensatoren jene Spannungs- Potentiale bestimmen, welche als analoge STQ(v)-Werte an Spannungs/ Frequenz- Konverter anzulegen sind, um an deren Outputs die digitalen Zeittaktfrequenzen zur adaptiven Messung der STQ(i)- und STQ(d)- Verstreichzeiten so zu modulieren, dass sie eine Funktion der Relativgeschwindigkeit vm bilden. In einer weiteren, nicht-mechanistischen Ausführungsform der Erfindung ist vorgesehen, dass sowohl die genannten Wahrnehmungsbereichszonen bzw. Schwellwertdetektoren sowie die beschriebenen STQ-Zeitquantisierungsprozesse nicht auf dieselbe Weise wie analog/ digitale Schaltkreise, sondern auf ähnliche Art wie molekular/biologisch/chemische Strukturen gebildet sind. In einer weiteren, allgemeinen Ausführungsform der Erfindung ist vorgesehen, dass die aktuell erfassten und gespeicherten STQ- Verstreichzeitdaten fortgesetzt mittels Echtzeit- Analyse mit früher erfassten und gespeicherten Zeitstrommustern verglichen werden, um dadurch externe Ereignisse oder physikalische Zustandsveränderungen mit einem Minimum an Redundanz identifizieren bzw. in Echtzeit erkennen zu können. In einer weiteren allgemeinen Ausführungsform der Erfindung ist vorgesehen, daß mit Sensoren und Einrichtungen zur o.g. Zeitstrommuster-Erkennung versehene, sich autonom bewegende Systeme, über Antriebs-, Lenkungs- und Bremsmechanismen verfügen, wobei die Regelung dieser Mechanismen derart erfolgt, daß das autonom bewegte System (insbes. ein Robotersystem) zuvor erkannte STQ- Zeitstrommuster in auto-adaptiver Weise zu reproduzieren vermag. Bei Wiederholung der Bewegung löscht eine Prozessoreinheit instabile oder ungenügend koordinierte Tempoverteilungsmuster aus dem Speicher und weist nur jene Zeitstrommuster als Instruktion zu, welche die Reproduzierung der Bewegung entlang gleicher Strecke in optimaler koordinierter Weise gewährleistet. Außerdem ist vorgesehen, die Zeitmessfrequenz für die genannte STQ(v)-Verstreichzeit- Messung in zeitlichem Maßstab proportional zu erhöhen oder zu vermindern, wodurch die Tempoverteilung in allen Bewegungen in selbem Maßstab proportioniert wird. Um die Messungen der besagten STQ-Verstreichzeitdaten gegebenenfalls zu korrigieren, und um die Erkennung identer Zeitstrommuster oder die Reproduzierung von Bewegungs- vorgängen zu verbessern, ist außerdem vorgesehen, die durch Schwellwertdetektoren gebildeten Wahrnehmungsbereichszonen automatisch nachzustellen bzw. zu fokussieren, falls es häufige Abweichungen erfordern. (Dies ist Gegenstand einer weiteren Patent- anmeldung).

	Kurzbeschreibung der Zeichnungen
		Fig. 1 zeigt ein Diagramm von SHANNON's deterministischer Methode der zeitdiskreten Quantisierung von Signalamplitudenverläufen. Figs. 2a-c zeigen graphische Diagramme der Quantisierung von Signalamplituden-Verläufen mittels Erfassung von STQ(v)-, STQ(i)- und STQ(d)- Verstreichzeiten nach der erfindungsgemäßen nicht-deterministischen Methode. Figs. 3a-cveranschaulichen diese nicht-deterministische Methode in Verbindung mit serieller Übertragung erfasster STQ(d)-Verstreichzeiten sowie mit Zeitzählfrequenz- Modulation der gleichfalls erfassten Parameter der momentanen Relativgeschwindigkeit (vm). Figs. 3d-g zeigen im Zusammenhang mit der beschriebenen Erfindung eine Methode des Vergleiches gegenwärtig erfasster STQ-Verstreichzeitsequenzen mit früheren erfassten und gespeicherten STQ- Verstreichzeitsequenzen, um Isomorphismus bestimmter Zeitstrommuster festzustellen. Fig. 4a zeigt eine molekular/biologische Methode der Quantisierung von STQ-Verstreichzeiten mittels sogenannter "Aktionspotentiale", die an Membranen von Rezeptor-Zellen produziert werden. Fig. 4b zeigt von einem Neuron (Rezeptorzelle) ausgehende, in vm-abhängiger Weise entlang der neuronalen Membran zur Synapse fortgeleitete Aktionspotentiale, wo die Kovarianz von STQ- Sequenzen analysiert wird. Fig. 4c zeigt eine Anzahl vm- abhängiger Aktionspotentiale, die von einer Gruppe entsprechender Rezeptorzellen entlang kollateraler Nervenfasern zu Synapsen fortgeleitet werden, wobei die zeitliche und räumliche Bahnung der AP's zusammen mit der Kovarianz dieser STQ- Sequenzen analysiert wird, um eine komplexe Wahrnehmung zu erkennen. Fig. 4d zeigt ein postsynaptisches Neuron, das Potentiale mit hemmenden Eigenschaften produziert. Fig. 4d zeigt ein postsynaptisches Neuron, das Potentiale mit hemmenden Eigenschaften produziert. Fig. 4e und Fig. 4f zeigen die prinzipielle Funktionsweise der synaptischen Übertragung von molekular/biologisch erfasster STQ- Information an andere Neuronen oder neuronale Verzweigungen. Fig. 5 zeigt eine Konfiguration, bei der die beschriebene erfindungsgemäßen Methode zur Generierung autonomer selbstorganisierender Mechanismen dient, und wobei die STQ- Verstreichzeiten auf elektronische Weise erfasst werden. Fig. 6a zeigt die Konfiguration einer einfachen Anwendungsform der erfindungsgemäßen Methode, in der die in Fig. 2a, 2b, 2c beschriebenen STQ(v), STQ(i), STQ(d)- Zeitdaten zur Erkennung bestimmter räumlicher Profile, Gebilde oder Strukturen angewandt werden, wobei sich das System mit beliebiger Geschwindigkeit fortbewegt. Figs. 6b-e zeigen verschiedene Diagramme und Tabellen im Zusammenhang mit der Anwendungsform in Fig. 6a, wobei die sensitive Abtastung und Erkennung eines bestimmten Profils wahlweise mit konstanter oder variabler Bewegungsgeschwindigkeit erfolgen kann. Fig. 7a - d zeigen verschiedene Sensor-Anordnungsformen und Sensor-Strukturen zur sensitiven Quantisierung von STQ(v)-Verstreichzeiten, welche zur Erfassung der Relativ- Geschwindigkeitsparameter dienen. Figs. 8a-f zeigt die Konfiguration sowie die Funktionsprinzipien einer weiteren Anwendungsform der erfindungsgemäßen Methode, bei der die Quantisierung von STQ- Zeitdaten (siehe Fig. 2a - 2c) zur Schaffung eines autonomen auto-adaptiven und selbstorganisierendenTrainingsroboters für den Einsatz im Sport dient. Dieser Roboter ist imstande, einen vom Benutzer vorgegebenen Bewegungsvorgang zu reproduzieren und optimieren. Er ist ebenso imstande, die ideale Spur und Tempoverteilung selbsttätig zu bestimmen, Abstände und Zeiten einzuhalten, Gefahrenszenarien zu erkennen und davor zu warnen, die Eigenbewegung sowie Geschwindigkeiten, Rundenzeiten, Teilzeiten, Gesamtzeiten und andere relevante Daten auf einem Monitor dazustellen. Zusätzlich ist der Trainingsroboter imstande, solche erfasste Daten in optischer oder akustischer Weise auszugeben. Fig. 9 zeigt in einer schematischen Darstellung die Produzierung von Zeitdatenströmen durch Signalamplitudenquerung bestimmter sensorischer Wahrnehmungsbereiche oder Empfindlichkeits-Zonen (bzw. Schwellwertpegel) in autonomen auto-adaptiven und selbstorganisierenden Strukturen, Organismen oder mechanistischen Robotiksystemen, wobei eine Vielzahl verschiedener Arten von Sensoren oder Rezeptoren vorhanden sein kann.
	Detailierte Beschreibung
		Fig. 1 zeigt ein Diagramm von SHANNON's deterministischer Methode der zeitdiskreten von Signalamplituden-Verläufen, welche mittels Analog/Digital-Wandler digitalisiert werden. Im allgemeinen technischen Sprachgebrauch wird diese Methode auch "Sampling" genannt. Diese deterministische Methode ist dadurch gekennzeichnet, dass erfasste Daten (a1, a2...an) mit bestimmten Zeitpunkten (T1, T2, T3,...Tn) korrelieren, die vom Program Counter eines Prozessors vorgegeben werden. In der gegenwärtigen Robotik-Praxis verlangt diese Methode sehr schnelle Prozessoren, hohe Samplingraten und eine hohe Anzahl redundanter Daten und Rechenoperationen bei deren Auswertung. Will man auf diese Weise Daten von Signalamplituden externer Quellen zum Zweck der Information über die räumliche Umgebung eines Systems, auf welchem ein sensor- gekoppelter Prozessor installiert ist, erwerben, so lässt SHANNON's Methode keine ausreichende Gewinnung von Daten über die momentane Relativgeschwindigkeit und die zeitlich/räumliche Zuordnung zu, die zum Zweck der Optimierung der Koordinierung der relativen Eigenbewegung notwendig wären. Eine Erkennung der eigenen Bewegung in Echtzeit ist daher nicht möglich. Aus diesem Grund ist diese Methode zur Generierung hocheffizienter autonomer Robotiksysteme zu schwach. 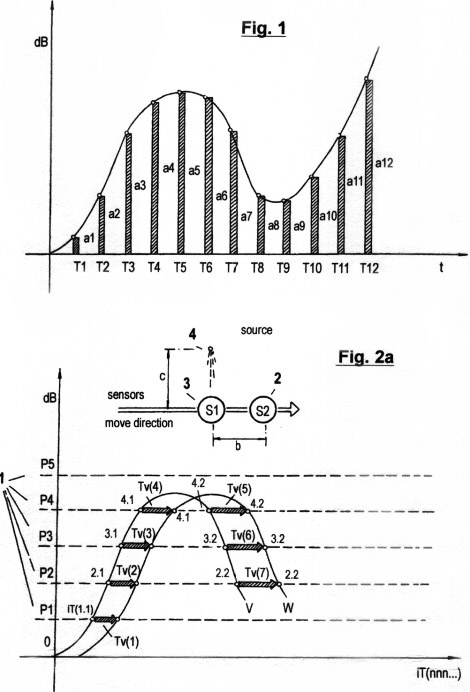Figs. 2a - c zeigen in drei verschiedene Graphen die sensorische Quantisierung von Signalamplitudenverläufen mittels der hierin beschriebenen erfindungsgemäßen Methode. Im Gegensatz zur in Fig. 1 gezeigten Quantisierungsmethode werden hierbei keinerlei "vertikalen Segmente" von Amplitudenverläufen abgetastet; sondern ausschließlich Verstreichzeiten gemessen, und zwar auf drei verschiedene, sich ergänzende Arten. Wie ersichtlich, müssen dazu eine gewisse Anzahl von Schwellwerten 1 (P1, P2...Pn) festgelegt werden, um sensorische Wahrnehmungsbereichzonen zu bilden. Jede Verweildauer und jedes Zeitintervall innerhalb der genannten Zonen wird ebenso erfasst wie die Verstreichzeit zwischen den Durchgängen von einem niederen zu einem höheren Schwellwert und umgekehrt. Fig. 2a zeigt die erste dieser drei verschiedenen Arten sensorischer Zeitquantisierung. Sie wird als STQ(v)- Verstreichzeitmessung (sensitive time quantum - velocity) bezeichnet und liefert ein Maß für die momentane Relativgeschwindigkeit vm. Man kann sie auch als Pausendauer zwischen zwei Phasendurchgängen zweier paralleler Signalverläufe an gleichen Schwellwertpotentialen verstehen. Nicht ganz korrekt ist dafür die übliche Bezeichnung "Phasenverschiebung". Im Graph sind die gemessenen STQ(v)-Verstreichzeiten mit Tv(n) bezeichnet. Die Phasendurchgänge an dem vom Sensor (bzw. vom Receptor) beim Vorbeibewegen an der entsprechenden externen Signalquelle 4 produzierten Amplitudenverlauf V sind mit iTv(n.m), die Phasendurchgänge an dem vom Sensor (bzw. Rezeptor beim Vorbeibewegen an der gleichen Signalquelle erhaltenen Amplitudenverlauf W mit iTw(n.m) zeichnet. Unter der idealen Voraussetzung, dass der räumliche Abstand (b) zwischen den beiden Sensoren 3, 4 im Vergleich zum Abstand c zwischen Signalquelle und Sensoren minimal ist, dass c beim Vorbeibewegen konstant bleibt, und dass beide Sensoren (bzw. Rezeptoren) identische Eigenschaften aufweisen und ein Analogsignal liefern, so werden an den Outputs der erwähnten Sensoren (bzw. der Sensor-Operationsverstärker) zwei Signalamplituden- Verläufe V und W produziert, die annähernd konruent sind. (Abweichungen von der Ideal-Konstellation können durch autonome Adaption des Sensorsystems in fortschreitend verbesserter Weise kompensiert werden; dies wird später beschrieben). Bewegt sich Sensor 2 in der bezeichneten Richtung entlang der Signalquelle so durchbricht die Signalamplitude V zunächst das definierte Schwellwertpotential P1 bei Phasendurchgang iTv(1.1). Die ansteigende Signalflanke startet einen ersten Zeitmesser zur Erfassung der ersten STQ(v)- Verstreichzeit Tv(1). Die weiter ansteigende Signalamplitude V durchbricht sodann die Schwellwertpotentiale P2, P3 und P4, wobei bei jedem Phasendurchgang weitere Zeitmesser zur Erfassung weiterer Verstreichzeiten Tv(2), Tv(3) und Tv(4) gestartet werden. Inzwischen hat sich Sensor 3 der Signalquelle 4 genähert und liefert den Signalamplitudenverlauf W. Durchbricht W bei Phasendurchgang iTw(1.1) das Schwellwertpotential P1, so stoppt die steigende Flanke den Zeitmesser zur Erfassung der ersten STQ(v)-Verstreichzeit Tv(1) und speichert sie. Derselbe Vorgang wiederholt sich für die Verstreichzeiten Tv(2), Tv(3) und Tv(4) beim Durchbrechen der nächsthöheren Schwellwert-Potentiale P2, P3 und P4. Beginnt die Signalamplitude V zu fallen, so durchbricht sie zunächst den Schwellwert P4 an der oberen Schulter des Amplitudenverlaufes nach unten. Nun startet die fallende Flanke einen Zeitmesser zur Erfassung der nächsten Verstreichzeit Tv(5). Bei den weiteren Phasen- durchgängen iTv(3.2) und iTv(2.2), bei dem die Schwellwerte P3 und P2 nach unten durch- brochen werden, werden ebenfalls wieder Zeitmesser durch die fallende Flanke gestartet, um die Verstreichzeiten Tv(6) und Tv(7) zu messen. Steigt der Verlauf der Signalamplitude V wieder an, so erfolgt die Erfassung der STQ(v)-Parameter wieder durch die steigende Flanke. Dasselbe gilt für das Stoppen der besagten Verstreichzeitmesser bei den Phasen- Durchgängen der parallel zu V verlaufenden Signalamplitude W. Fig. 2b zeigt eine weitere Art sensorischer STQ- Zeitquantisierung. Sie wird als STQ(i)- Verstreichzeitmessung (sensitive time quantum - interarrival) bezeichnet. Vereinfacht, bedeutet sie die benötigte Zeit Tw für die Zurücklegung einer relativen Strecke. Man kann sie auch als Verweildauer eines Signalverlaufes zwischen den Phasendurchgängen an gleichen Schwellwertpotentialen verstehen. Wird die Zeitzählfrequenz für ihre Messung proportional zu Relativgeschwindigkeits-Parameter Tv (bzw. zu STQ(v)- Verstreichzeiten) beschleunigt oder vermindert, so korrelieren die gezählten und gespeicherten modulierten Impulse mit der relativen Strecke. Besteht absolute Invarianz zwischen dem Sensor und den Signalquellen (auch "Synchronität" genannt), so kann kein STQ(i)-Parameter erfasst werden; ändert sich jedoch die Signalintensität, so können STQ(i)-Verstreichzeiten auch dann erhalten werden, wenn keine Relativbewegung stattfindet. Während einer Bewegung sind sie also nicht nur zur Erfassung von variablen Signalen erforderlich, sondern auch zum Abtasten der räumlichen Umgebungen. Im Graph (Fig. 2b) sind die gemessenen STQ(i)-Verstreichzeiten mit Tw(n) bezeichnet. Die Phasendurchgänge, welche vom Amplitudenverlauf W produziert werden, wenn sich Sensor (bzw. Rezeptor) 5 entlang den entsprechenden benachbarten Signalquel- len 6 und 7 vorbeibewegt, sind mit iTw(n.n) bezeichnet. Sobald sich Sensor (bzw. Rezeptor) 5 in der bezeichneten Richtung entlang der Signalquelle 6 bewegt, durchbricht die Signal- Amplitude W zunächst das Schwellwertpotential P1 bei Phasendurchgang iTw(1.1). Die steigende Signalflanke startet einen ersten Zeitmesser zur Erfassung der ersten STQ(i)- Verstreichzeit Tw(1). Danach durchbricht die weiter ansteigende Signalamplitude W die vorgegebenen Schwellwertpotentiale P2, P3 und P4, wobei bei jedem Phasendurchgang Zeitmesser gestartet werden, um weitere Verstreichzeiten Tw(2), Tw(3), Tw(4).... zu erfassen. Inzwischen beginnt sich Sensor 5 aus dem Bereich der Signalquelle 6 zu entfernen. Die fallende Signalamplitude W durchbricht zunächst das Schwellwertpotential P4, worauf beim Phasendurchgang iTw(4.2) nun die fallende Flanke jenen Zeitmesser stoppt, der zur Erfassung der STQ(i)-Verstreichzeit Tw(4) gestartet worden war. Gleichzeitig startet dieselbe fallende Flanke einen weiteren Zeitmesser, der die Verstreichzeit Tw(5) bis zum Eintreffen der nächsten ansteigenden Flanke misst. Jedoch erscheint diese steigende Flanke erst beim Vorbeibewegen des Sensors 5 an der entsprechenden Signalquelle 7. Vorher fällt die Signal- Amplitude W aber bis unter die Schwellwerte P3 und P2, bei deren Phasendurchgang iTw(3.2) und iTw(2.2) die Zeitmesser zur Erfassung der STQ(i)- Verstreichzeiten Tw(3.2) und Tw(2.2) gestoppt werden. Gleichzeitig werden weitere Zeitmesser zur Erfassung der Verstreichzeiten Tw(6) und Tw(7) gestartet. Sie stoppen wiederum zu den Phasendurchgängen iT(2.3), iTw(3.3), iTw(4.3) und iTw(5.1), wenn die Signalamplitude wieder fällt (jedoch nicht vor dem Vorbeibewegen des Sensors an Signalquelle 7). Nach diesen Phasendurchgängen starten neue Zeitmesser zur Erfassung der nächsten Verstreichzeiten Tw(8), Tw(9), Tw(10), Tw(11), usw.   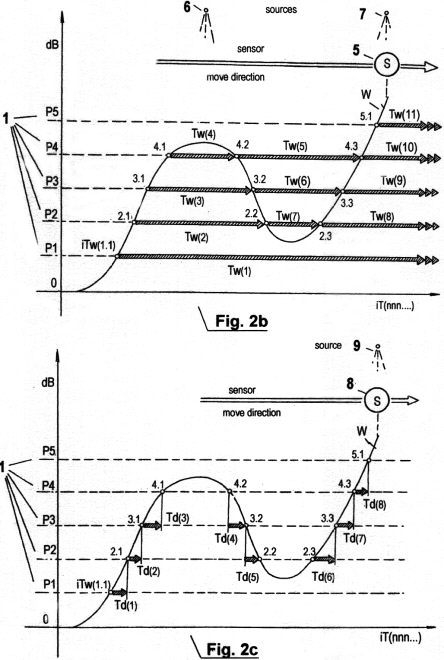Fig. 2c zeigt eine dritte Art der sensorischen Zeitquantisierung, die sich von den in Fig. 2 und Fig. 2b gezeigten Methoden total unterscheidet. Sie wird als STQ(d)- Verstreichzeit- Messung (sensitive time-quantum - differential) bezeichnet. Man kann sie auch als Verweil- Dauer Td, gemessen zwischen einem ersten Phasendurchgang bei einem ersten bestimmten Schwellwertpotential und einem zweiten Phasendurchgang bei einem zweiten bestimmten Schwellwertpotential verstehen, das um eine Stufe höher oder niedriger als das Erstere ist. STQ(d)- Verstreichzeiten sind Parameter für die Flankensteilheit von Signalamplituden, und somit auch für deren Frequenz. Mittels schnellem Vergleich von STQ(d)-Verstreichzeiten können Signalverläufe in Echtzeit erkannt werden. Sie sind daher zur Schaffung intelligenter Verhaltensweisen ebenso unerläßlich wie STQ(v) oder STQ(i)-Quanten. Die Quantisierung von STQ(d)- Zeitdaten ist unter allen physikalischen Zuständen und beliebigen Relativ- Bewegungen zwischen Sensor und externen Quellen möglich, in welchen STQ(v)- und STQ(i)- Verstreichzeiten ebenfalls quantisierbar sind. Werden die STQ(d)-Verstreichzeiten kumulativ und in Serie erfaßt, so können sie zur Verifizierung und Plausibilitätsprüfung von (gleichfalls erfassten) STQ(i)-Verstreichzeiten dienen. Im Graph (Fig. 2c) sind die gemessenen STQ(d)- Verstreichzeiten mit Td(n) bezeichnet. Die Phasendurchgänge, welche vom Amplitudenverlauf W produziert werden, wenn sich Sensor (bzw. Rezeptor) 8 im Bereich der Signalquelle 9 befindet, mit iTw(n.n) bezeichnet. Bewegt sich Sensor 8 in der gezeigten Richtung entlang der Signalquelle 9, so durchbricht die Signalamplitude W zunächst das definierte Schwellwert- Potential P1 bei Phasendurchgang iTw(1.1). (Dies geschieht bei aktivem bzw. variablem Signalquellenfeld selbstverständlich auch dann, wenn Sensor und korrespondierende Signal- quelle in invarianter Position zueinander sind). Die steigende Signalflanke startet einen ersten Zeitmesser zur Erfassung der ersten STQ(d)- Zeitdate. Wenn der weiter ansteigende Amplitudenverlauf W das nächsthöhere Schwellwertpotential P2 beim Phasendurchgang iTw(2.1) durchbricht, so wird dieser Zeitmesser gestoppt und die gemessene STQ(d)- Verstreichzeit Td(1) gespeichert. Gleichzeitig startet der nächste Zeitmesser zur Erfassung und Speicherung der Verstreichzeit bis zum nächsten Phasendurchgang bei iTw(3.1), wo er gestoppt wird; dann wird der nächste Timer aktiviert bis zu iTw(4.1), wo er ebenfalls gestoppt wird usw. Beim Phasendurchgang iTw(4.1) durch Schwellwertpotential P4 wird der nächste Zeitmesser gestartet. Da aber das Signal kein nächsthöheres Schwellwertpotential mehr erreicht bevor es wieder gegen P4 absinkt, kann mit letzterem Zeitmesser keine STQ(d)- Verstreichzeit erfasst werden. Nur die Quantisierung von STQ(i)-Verstreichzeiten, wie in Fig. 2b beschrieben, kann in dieser Situation stattfinden. Die nächste STQ(d)- Verstreichzeit Td(4) wird erst dann erfasst, wenn die Signalamplitude bei iTw(4.2) unter den Schwellwert P4 geht, wonach ein weiterer Timer startet, der beim Phasendurchgang durch den um eine Stufe niedrigeren Schwellwert P3 gestoppt wird. Gleichzeitig wird der nächste Zeitmesser gestartet usw. In mechanistischen Anwendungen, wo die Analyse von Signalamplituden die Quantisierung von STQ(d)-Verstreichzeiten erfordert, werden STQ(d)- Daten oftmals in Kombination mit STQ(i)-Daten aquiriert. Besteht die Intention der Anwendung dieser Quantisierungsmethode darin, einem Roboter die Erkennung seiner Eigenbewegung aus subjektiver Sicht zu ermög- lichen (durch Aufspüren und Abtasten der räumlichen Umgebung beim Bewegen entlang externer Signalquellen), so werden überwiegend STQ(v)- und STQ(i)-Daten erfasst. Geht jedoch der Schwerpunkt in Richtung Erkennung instabiler optischer oder akustischer Quellen, wie etwa Bilder, Musik oder Gespräche usw., so nimmt der Anteil von STQ(d)-Verstreichzeiten zu, während der Anteil von STQ(v)-Parameter abnimmt. Findet keinerlei relative Bewegung statt, so können auch keinerlei Geschwindigkeitsparameter von irgendwelchen Sensoren abgeleitet werden; nur die Quantisierung von STQ(d)- und STQ(i)-Verstreichzeiten ist möglich. Figs. 3 a - c zeigen einen wichtigen Aspekt der Gestaltung der beschriebenen Methode im Zusammenhang mit serieller Übertragung von erfaßten STQ(d)-Verstreichzeiten sowie in Verbindung mit Zeitzählfrequenzmodulation in Relation zu simultan erfassten STQ(v)- Parametern, die für die momentane Relativgeschwindigkeit (vm) stehen. Diese Gestaltungs- form der Methode eignet sich allerdings nur dort, wo überwiegend STQ(d)-Verstreichzeiten gemessen werden; zusammen mit solchen STQ(i)-Verstreichzeiten (siehe auch Beschreibung zu Fig. 2c), welche bei den Phasendurchgängen des erreichten maximalen Schwellwerts nahe des Maximums der Amplitude, oder des erreichten minimalen Schwellwerts nahe des Minimums der Amplitude, produziert werden. In diesem Fall können alle gemessenen Verstreichzeiten als serielle Sequenzen dargeboten werden. Werden hingegen zu jedem Schwellwertpotential STQ(d)- und bzw. nur STQ(i)-Verstreichzeiten erfasst (siehe Beschreibung zu Fig. 5), so fallen diese Daten parallel an und müssen auch parallel verarbeitet werden.   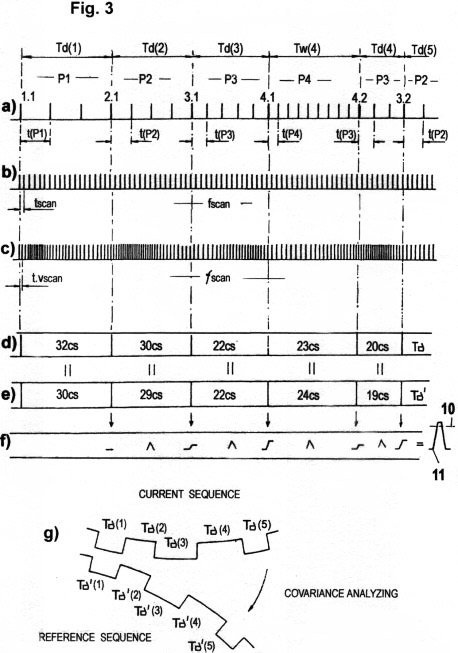Fig. 3a zeigt, wie eine einfache serielle Impulsfolge zum schnellen Datentransfer der erfassten STQ(d)- Verstreichzeiten ausreicht, wenn die Schwellwertpotentiale P1, P2, P3..., welche jene Phasendurchgänge 1.1, 2.1, 3.1...bestimmen, von denen die STQ-Verstreich- zeiten abgeleitet werden, entweder durch Codes oder durch bestimmte charakteristischen Frequenzen "markiert" sind. Im gezeigten Fall sind diese "Marker" Impulsfolgen mit Perioden t(P1), t(P2), t(P3) ...und Frequenzen f(P1), f(P2), f(P3).... Ihre Modulation erfolgt in Abhängigkeit von den entsprechenden Schwellwertpotentialen. Diese Identifikations- Impulsfolgen (IP) dienen der Identifizierung der bestimmten Schwellwerte P1, P2, P3...(bzw. der Wahrnehmungsbereichszonen 1, 2, 3...). Erst die zusammen mit diesen Identifikations- Impulsen (IP) operierenden invarianten Zeitzählimpulsen (ITPC) mit der Periode tscan (Fig.3b) oder variablen Zeitzählimpulsen (VTPC) mit der Periode t.vscan (s. Fig. 3b, 3c) bewirken die eigentliche Erfassung von STQ(d)-Verstreichzeiten Td(1), Td(2), Td(3), Td(4)... (oder bzw. der STQ(i)- Verstreichzeiten Tw(1), Tw(2), Tw(3), Tw(4)..., welche nahe der Amplituden- Maxima und -Minima auftreten) nach dem bereits beschriebenen Beispiel. Variable VTCP- Impulsfolgen mit der Periode t.vscan, welche automatisch in Relation zu den erfassten STQ(v)-Verstreichzeiten (d.h. zur augenblicklichen Momentangeschwindigkeit vm) moduliert sind, werden dazu verwendet, um von externen Quellen erhaltene Signalamplituden in geschwindigkeits-proportionaler Weise abzutasten. Dies reduziert die Redundanz der Rechen- prozesse erheblich (s. auch Fig. 3c). Die solchermaßen durch VTCP-Impulse vm-adaptiv erfassten STQ(d)-Verstreichzeiten werden mit Tδ(1,2,3,....), die in derselben Weise erfassten STQ(i)-Verstreichzeiten mit Tω(1,2,3...) bezeichnet. Figs. 3b zeigt die Messung von STQ(d)-Verstreichzeiten mit invarianten ITPC-Impulse mit der Periode tscan und mit einer konstanten Frequenz fscan. Dies ist der Fall, solange keine STQ(v)- Parameter erhalten werden, d. h. wenn keine Relativbewegung zwischen Sensor und Signalquelle auftritt und daher auch keine Relativgeschwindigkeit (vm) gemessen werden kann.   Figs. 3c zeigt die Messung der Verstreichzeiten mit modulierten VTCP-Impulsen. Diese Zeitzählimpulse sind abhängig von der momentanen Relativgeschwindigkeit vm (bzw. vom erfassten STQ(v)- Parameter), und zwar in einer Weise, dass ihre Periode (t.v)scan und Frequenz ƒscan proportional zu vm ist. Wenn vm sehr klein ist oder gegen Null geht, so sinkt die Zählfrequenz ƒscan gleichfalls ab bis zur Minimalfrequenz fscan (wie in Fig. 3b). Wie in Fig. 2a gezeigt, wird jeder STQ(v)- Geschwindigkeitsparameter mittels eines zweiten adäquaten "vorauseilenden" Sensors (bzw. Rezeptors)erfasst. Somit ist vm schon vor der eigentlichen STQ(d)- und/oder STQ(i)- Verstreichzeitmessung festgehalten. Es ist daher möglich, ƒscan zur Messung der Td(1,2...n)-Zeitdaten entsprechend den erfassten STQ(v)- Parametern zu modulieren, um so die Zahl von t.v- Kalkulationen zu reduzieren sowie erforderlichen Speicherplatz zu minimieren. Daraus resultiert ein weitgehend redundanzfreier Analyseprozeß. Obwohl die mit dieser Methode gezählten Zeitimpulse annähernd kovariant mit der relativ zurückgelegten Strecke (d) sind, stellen sie dennoch nachweislich modifizierte Zeitdaten dar und nicht Distanzmaße. Wie auch die Entstehung dieser Daten, so erfolgt auch die weitere Verarbeitung und Analyse solcher modifizierter STQ-Verstreichzeiten nach probabilistischen Prinzipien. Die besagten Zeitdaten werden quasi "subjektiv empfunden". In mechanistischen Systemen geschieht die annähernd weg-proportionale Modulation der Zeit- zählfrequenzen überwiegend mittels programmierbare Oszillatoren und Timer, wie aus Fig. 5 ersichtlich ist. Hingegen wird dieser adaptive Prozess (ein Teil der sogenannten "autonomen Adaption") in komplex strukturierten biologisch/ chemischen Organismen oft durch proportionale Änderung der Fortleitungsgeschwindigkeit von Zeitmessimpulsen in neuronalen Fasern erzielt, wie dies in Fig. 4a, 4b, 4c und 4d gezeigt wird. Autonome Adaption und adaptive Zeitbasisänderungs-Prozesse der beschriebenen Art können aber auch anders gestaltet sein. Sie können auf molekularer, atomarer und subatomarer Ebene existieren. Der Patentanmelder bezeichnet dieses Prinzip als "zeitliche Auto-Adaption. Fig. 3d - f zeigen die konzeptionelle Basis für den Vergleich von aktuell erfasster STQ-Zeitdatensequenzen mit früher registrierten STQ- Zeitdatensequenzen, sowie ihre Analyse auf statistischer Grundlage. Die vm-modulierten, in Fig. 3d gezeigten Zeitdaten Td(n...) mit der Reihe 32-30-22-23-20 (cs= Zählzyklen) werden Date für Date mit früher registrierten, gleichfalls in vm-modulierter Weise erfassten Td'-Zeitdaten der Reihe 30-29- 22-24-19 verglichen. Der Vergleichsprozeß ist genau genommen eine Kovarianzanalyse. Wenn die Regressionskurven beider Zeitdatenreihen konvergieren, so besteht Kovarianz. In mechanistischen Systemen kommen zu diesem Zweck Koinzidenz-Meßsysteme, Komparator- Schaltkreise, Software für statistische Analysen oder auch "Fuzzy-Logic" zum Einsatz. Die Wahrscheinlichkeitsdichte-Parameter werden summiert, und sobald der Gesamtwert innerhalb einer bestimmten Periode eine vorgegebene Schwelle 10 übersteigt, wird ein Signal 11 produziert, welches anzeigt, dass die Sequenz "erkannt" worden ist. Dieses Signal dient vorwiegend zur adaptiven Regelung der Aktuatoren in mechanistischen Systemen (bzw. zur Motorik in Organismen). Weiters zeigt das Signal an, dass "autonome Adaption" an die registrierten Zeitdatenmuster stattgefunden hat. Was das motorische Verhalten irgendeines mechanistischen oder biologischen Mechanismus betrifft, so ist es klar, dass die Erkennung von Signalfolgen Hand in Hand mit automatischer Anpassung bzw. autonomer Adaption geht. Dieses Prinzip sei hiermit als "motorische Auto-Adaption" oder "Auto- Emulation" bezeichnet. Fig. 3g zeigt diesen Autoadaptions-Prozess in schematischer und leicht verständlicher Weise. Eine aktuell erfasste Td- Zeitdatensequenz wird fortgesetzt mit einer früher erfassten Td'- Zeitdatensequenz verglichen, und besteht annähernde Übereinstimmung, so passen die Sequenzen zueinander wie Schlüssel und Schloss. Wie aus den folgenden Beschreibungen ersichtlich, schafft dieser Vorgang eine Art "Bootstrapping-Prozess" bzw. ein "motorisches Nacheiferungsbestreben", das eine grundlegende Eigenschaft aller redundanzfreien autonomen selbstorganisierenden Systeme bzw. eines Organismus darstellt. Zwar ist die Konvarianzanalyse zweier Zeitdatenmuster in mechanistisch/elektronischen Systemen relativ aufwendig (s. dazu Fig. 5); dies gilt jedoch nicht für molekular/biologische Organismen und andere Einheiten. In solchen Systemen tritt dieses "Bootstrapping" als "synergetischer Effekt"auf - annähernd vergleichbar mit dem Rollen einer Anzahl von Billardkugeln in eine Reihe von Löchern, die ein Muster bilden. (Die Bezeichnung "Synergetik" wurde übrigens erstmals von H. HAKEN im Jahre 1970 eingeführt). Das erfolgreiche Einlochen wird von Geschwindigkeit und Richtung bestimmt. Ändern sich diese Parameter, so erfolgt kein Einlochen. Ein Versuch kann ebenfalls scheitern, wenn sich die Position der Löcher irgendwie verändern würde, während die Abstoß-Positionen der Kugeln konstant blieben; selbst dann, wenn ihre Geschwindigkeit und Richtung kovariant mit den urprünglichen Parametern wäre (und wobei die Kovarianz die Änderung der Muster nicht entsprechend berücksichtigt). In ähnlicher Weise prägt eine aktuelle STQ- Zeitdatensequenz, die von einem autonomen selbstorganisierenden System erfasst wurde, ein bestimmtes charakteristisches Finger- abdruckmuster, und sooft ein früher registriertes Referenz-Muster gefunden wird, das isomorph mit einem aktuell registrierten Muster ist, so resultiert daraus Auto-Adaption und Auto-Emulation (Nacheiferungsbestreben). Dieses Phänomen wohnt als teleologisches Ordnungsprinzip allen Lebensformen, Organismen und elementaren Strukturen inne. Findet sich kein kovariantes referentes Muster, so kollabiert die auto-adaptive Regulation und das System verhält sich chaotisch. Der Zustand geht erst dann wieder vom Chaos zur Ordnung über, wenn aktuell erfasste STQ-Zeitmuster wieder mit früher erfassten STQ- Zeitmuster zu konvergieren beginnen, die vom Analysator als "kovariant" befunden werden. Figs. 4a - d illustrieren ein Modell der Erfassung und Verarbeitung von STQ(d)- und STQ(v)- Verstreichzeiten (s. auch Fig. 3a - g) - sowie zur zeitlichen und motorischen Auto-Adaption - in molekular/biologischem Zusammenhang. Die grundlegenden Elemente des Modells sind in der Neurophysiologie bereits von KATZ, GRAY, KELLY, REDMAN, J. ECCLES u. a. beschrieben worden. Die vorgestellte Erfindung ist aber deshalb von besonderer Neuheit, weil hier zum ersten Mal zeitliche und motorische Auto-Adaption auf Basis von STQ-Quanten beschrieben wird. Derartige Systeme bestehen zumeist aus einer Vielzahl von Neuronen (Nervenzellen). Diese Neuronen kommunizieren mit Rezeptoren (sensorischen Neuronen), welche die Erfas- sung und Erkennung der ihrer physikalischen Umgebung ermöglichen. Zusätzlich kooperieren sie auch mit Effektoren (Muskeln etc.) die als ausführende Organe für die motorische Aktivi- tät dienen. Der Ausdruck "Rezeptor" oder "sensorisches Neuron" entspricht dem mechanisti- schen Begriff "Sensor". Ein "Effektor" ist dasselbe wie ein "Aktuator", wie man ihn aus der Kybernetik-Literatur kennt. Jedes Neuron besteht aus einer Zellmembran, die den Zellkern und den Zellinhalt umschließt. Eine unterschiedliche Anzahl von Fortsätze aus den Neuronen, (Axone, Dendriten) leitet Information zu Effektoren oder anderen Neuronen weiter. Die Verbindungsstelle einer dendritischen oder axionalen Endigung mit einer anderen Zelle wird "Synapse" genannt. Die Neuronen selbst können als komplexe biomolekulare Sensoren und Zeittaktgeber aufgefasst werden; die besagten Synapsen als Zeitdatenanalysatoren, welche die aktuell registrierten Verstreichzeitsequenzen fortgesetzt mit früher registrierten Verstreich-Zeitmustern vergleichen, welche von den sensorischen Neuronen (Rezeptoren) produziert und entlang Nervenfasern zu den Synapsen weitergeleitetet werden. Dort erfolgt eine Art von "Kovarianz-Analyse", und es werden entsprechende Wahrscheinlichkeitsdichte- Signale generiert, die an benachbarte neuronale Systeme oder an Effektoren geleitet werden. Fig. 4a zeigt ein sogenanntes "Aktionspotential" AP, das durch eine abrupte Änderung der Verteilung von Natrium-Ionen und Kalium-Ionen zwischen dem intrazellulären und extrazellulären Lösungsgemisch entsteht, welches wie ein Kondensator arbeitet. Diese Ionen-Konzentrationen behalten ein bestimmtes Gleichgewicht, solange kein Stimulus an der Rezeptor-Zelle auftritt. In diesem Gleichgewichts-Zustand ist ein konstantes negatives Potential 12 an der Zell-Membran vorhanden, das "Ruhe-Potential" genannt wird. Sobald ein Rezeptor einen Stimulus aus einer externen Signalquelle wahrnimmt, fließen Na+ Ionen in die neuronale Zelle und bewirken, dass sich die Verteilung positiver und negativer Ionen plötzlich umkehrt, und die Zell-Membrane "depolarisiert" wird. Je nach Intensivität dieses Rezeptor-Reizes entstehen nun folgende Effekte:   (a) Wird die Schwelle P1 nicht erreicht, so entsteht ein sogenanntes "elektrotonisches Potential"     EP, das sich entlang der Zell-Membran (bzw. der axonalen Faser) passiv fortpflanzt, und     in bezug auf zurückgelegte Zeit und Ort seines Auftretens exponentiell abnimmt.     Die Produzierung eines EP ist vergleichbar mit dem Anzünden einer leeren Zündschnur.     Das Feuer wird sich ein Stück weit ausbreiten, dann im weiteren Verlauf schwächer werden     und schließlich verlöschen. EP's entstehen bei jeder Reizung eines Neurons. (a) Wird die Schwelle P1 überschritten, so entsteht ein "Aktionspotential" AP (wie in Fig. 4a),     das sich entlang der Zell-Membran (bzw. der axonalen Faser) mit konstanter Amplitude in     selbstregenerierender Weise fortpflanzt. Die Produzierung eines AP ist vergleichbar mit     dem Auftreten eines Funkens an einer intakten Zündschnur; das entflammte Zündpulver     erhitzt benachbarte Abschnitte der Zündschnur soweit, dass dort das Pulver ebenfalls     entflammt usw., wodurch sich die Flamme entlang der Zündschnur fortpflanzt. AP's werden zur Quantisierung von STQ(d)- und STQ(v)-Verstreichzeiten verwendet. Sie sind praktisch äquivalent zu jenen Identifikations-Impulsen IP mit den Perioden t(P1), (t(P2), (t(Pn)..., welche in Fig. 3a gezeigt werden. AP's zeigen das Auftreten von Phasen- Übergängen an, von denen STQ(d)-STQ(v)- Verstreichzeiten abgeleitet werden. Zusätzlich bewirken sie indirekt die Aktivierung molekular/biologischer "Zeitmesser" zur Aufnahme solcher Zeiten. AP's stellen jedoch weder deterministische Samplingraten für irgendeine Amplitudenabtastung dar, noch entsprechen sie elektronischen Spannungs/Frequenz- Wandlern. Außerdem ist ihre Amplitude unabhängig von der Reizintensivität am Rezeptor, und sie stellen auch keinerlei Zeittakt-Impulse für die Messung von Verstreichzeiten dar. Hingegen wird die Erfassung solcher STQ-Verstreichzeiten von den Geschwindigkeiten beeinflusst und moduliert, mit denen die Aktionspotentiale sich entlang den Nerven-Fasern (Axonen) und den Membran-Distrikten fortpflanzen. Die zeitmessenden Eigenschaften von AP's werden hier wie folgt detailliert beschrieben: Wenn ein EP - in Antwort zu einem Rezeptor-Reiz - einen bestimmten Schwellwert (P1) 13 überschreitet, dann löst es ein AP 16 aus. Der Amplitudenverlauf eines AP fängt mit dem Aufstrich 14 an und endet mit der Repolarisation 15, beziehungsweise mit der sogenannten "Refraktärphase". Nach dem Ende dieses Vorganges kehrt das Membran-Potential wieder zum Ruhepotential P0 zurück, und die Ionen-Verteilung gelangt wieder ins Gleichgewicht. Nicht jeder Rezeptor-Stimulus erzeugt genügende elektrische Leitfähigkeit, um ein AP zu produzie- ren. Solange er unter einer Minimalschwelle P1 bleibt, erzeugt er nur das zuvor erwähnte elektrotonische Potential EP. (Für ein besseres Verständnis von Verstreichzeitmessungen in biologisch/chemischen Modellen betrachte man nochmals Fig. 2c und Fig. 3a): Das erste AP, das nach Stimulieren eines Receptors ausgelöst wird, erzeugt zunächst (indirekt) jenen Impuls, der den ersten Zeitmesser zur Aufnahme der ersten STQ(d)- Verstreichzeit aktiviert, wenn die Signalamplitude W das Schwellwert-Potential P1 bei Phasenübergang iTw(1.1) durchbricht. Gleichzeitig stellt es auch einen Identifikations-Impuls IP dar. Das erste AP entspricht quasi dem ersten IP aus einer Reihenfolge von IP 's, die den jeweiligen Status des Schwellenwerts (oder Wahrnehmungbereichs) anzeigen, wo sich die Stimulations- Intensitivität gerade befindet. So lange der Rezeptor-Reiz bestehen bleibt, wiederholt sich ein AP 16a, 16b... in zeitlichen Intervallen, deren Periode von der Höhe des jeweiligen Schwellwertes abhängt, in dem sich der Stimulus gerade befindet. Diese Intervalle entsprechen jenen IP- Perioden t(P1), t(P2)... welche für die serielle Zuordnung und Verarbeitung von STQ- Verstreichzeiten erforderlich sind (s. Fig. 3a). Die AP-Frequenz wird stabilisiert durch die sogenannte "relative Refraktärphase" (Ausfallzeit) nach jedem AP, während derer keine neue Depolarisation möglich ist. Weil sich die Refraktär- Phase in adaptiver Weise proportional zu einer zunehmenden Reiz-Intensität beim Rezeptor verkürzt (z. B. wenn das EP einen höheren Schwellwert P2 bzw. Wahrnehmungs-Bereich 13a erreicht), besteht demnach eine Ähnlichkeit zu einem "programmierbaren bistabilen Multivibrator" wie er in der mechanistischen Elektronik zu finden ist. Der Verlauf dieser Ausfallzeit ("Refraktorität") nach einem AP folgt der strichpunktierten Linie 19. Fig. 4a zeigt, daß es nach dem Ende einer Repolarisation eine "absolute Refraktoritäts-Periode" t(tot) gibt. Kein neues AP kann während dieser Zeit ausgelöst werden; egal, wie hoch die Reiz- Intensität am Rezeptor steigt. Auf diese Weise ist das "maximale Ausmaß" einer gerade noch wahrnehmbaren Reizintensität programmiert. Wichtig ist die Tatsache, dass sowohl die Dauer der relativen Refraktärphase als auch die Charakteristik der absoluten Refraktoritätsphase auto-adaptiven Gesetzmäßigkeiten unterworfen sind, und sich daher kontinuierlich an neu auftretende Zustandsveränderungen im Organismus anpassen. Das bedeutet, dass auch jene Schwellwerte P0, P1,...., aus denen STQ-Quanten abgeleitet werden, keine absoluten Größen sind, sondern adaptiven Veränderungen unterliegen, wie alle anderen Parameter, insbes. "Zeit", auch. Nun wird erklärt, was nach der Registrierung einer erster STQ(d)-Verstreichzeit bei P1 durch das erste "AP" weiter geschieht: Steigt die Reizintensität (mit einer theoretischen Amplitude W) von der niedrigeren Schwelle P1 zu einer nächsthöheren Schwelle P2 an, dann verursacht das nächste folgende AP indirekt die Registrierung der zweiten STQ(d)- Verstreichzeit, sobald der Phasenübergang durch die nächsthöhere Schwelle P2 erfolgt. Derselbe Vorgang wiederholt sich in Hinsicht auf die Schwellwerte P3, P4 usw. In jedem Fall fungiert das AP gleichzeitig als Identifikations- Impuls IP, wie zu Fig. 3a beschrieben. Es wiederholt sich deshalb in schwellwert-abhängigen Perioden solange, als eine Wahrnehmung auf den Rezeptor einwirkt (bzw. solange der Rezeptor etwas "wahrnimmt"). Als Beispiel sei Fig. 3a betrachtet: Solange die Reizintensität in Zone P2 verweilt, kehrt das AP 17, 17a, 17b... in kurzen zeitlichen Perioden wieder. Diese Perioden (oder Intervalle) entsprechen jenen der IP-Identifikations-Impulse mit der Periode t(P2), welche zur seriellen Registrierung der STQ-Verstreichzeiten Td(2) und Tw(2) erforderlich sind. Erreicht die ansteigende Reizintensität den Schwellwert P3 (bzw. die Wahrnehmungsbereichszone 3) 13b, dann wiederholt sich das AP 18a, 18b, 18c... in noch kürzeren Zeitperioden. Dies entspräche jenen IP-Identifikations-Impulsen mit der Periode t(P3) in Fig. 3a , welche indirekt für das serielle Timing der STQ-Verstreichzeiten Td(3) und Tw(3) erforderlich sind. Eine noch größere Reizintensität, zum Beispiel in P4 (oder in Zone 4), würde eine noch kürzere Periode von AP 's erzeugen. Dies entspräche etwa t(P4) in Fig. 3a. Die maximal mögliche AP-Impuls- Frequenz wird jedoch von t(tot) bestimmt. Kürzere Refraktäritäts-Phasen nach der Depolarisation von APs produzieren auch kleinere AP-Amplituden. Diese Eigenschaft vereinfacht die Zuordnung von AP 's zusätzlich. Im folgenden Teil wird die Generierung der eigentlichen Zeitzählimpulse für die STQ- Quantisierung beschrieben. Diese Zeitzählimpulse sind entweder invariable ITPC oder vm- proportionale VTCP wie sie in Fig. 3a gezeigt wurden. Wie erwähnt, sind die Zeitzählimpulse für das Quantisieren von Verstreichzeiten durch jene Geschwindigkeit bestimmt, mit dem sich ein AP entlang eines Axons fortpflanzt. Diese Geschwindigkeit hängt weiters ab vom Ruhe- potential und von der Menge des Na+ Ionen-Stroms in den intrazellulären Raum beim Beginn des Depolarisations-Prozesses, sobald die Wahrnehmung an der Rezeptor-Zelle einen elektrischen Strom verursacht, der das extra/intra-zellulare Ionen-Gleichgewicht beeinflusst. Am Beginn der Stimulation eines Rezeptors (dem Ausgangspunkt der Wahr- nehmung), fließt nur kapazitiver Strom vom extra-zellularen Raum zur intra-zellularen Flüssigkeit. Dies ruft das besagte "elektrotonische Potential " EP hervor, der sich passiv fortpflanzt. Erst dann, wenn dieses EP die Schwelle P1 überschreitet, wird ein AP produziert, das sich in selbstgenerierender Weise entlang den Membran-Distrikten fortpflanzt. Je mehr kapazitiver Strom noch nach der Depolarisation (bzw. Umladung) des Membran-Kondensators während der Stimulus-Initialisierung verfügbar ist, desto größer ist die Na+-Strömung in den intra-zellularen Raum, und desto mehr EP-Strom kann in noch nicht depolarisierte Gebiete fließen. Auf diese Weise wird das Tempo weiterer Depolarisations-Prozesse in den Nerven- fasern, und somit auch die Fortpflanzungsgeschwindigkeit der weiteren AP's, proportional erhöht. Die Umladungszeit des Membran-Kondensators ist also jener Parameter, der die Größe des Ruhepotentials 12 bestimmt. Startet ein Reiz vom niedrigsten Ruhepotential P0 12 aus, so ist der Na+ Einstrom am größten, der Anstieg des EP ist am steilsten und seine elektro- tonische Ausbreitung ist am schnellsten. Wird ein AP ausgelöst, dann ist in diesem Fall auch seine Fortleitungsgeschwindigkeit maximal. Aber wenn ein Rezeptor-Stimulus von einem höheren Potential 12a, 12b oder 12c... startet, dann ist der Na+ Einstrom teilweise in- aktiviert, und es nimmt die Steilheit des EP-Anstiegs sowie die Ausbreitungsgeschwindigkeit des elektrotonischen Flusses ab. Deshalb nimmt auch die Fortpflanzungsgeschwindigkeit eines AP ab. Diese besonderen Eigenschaften werden in molekular/biologischen Modellen benutzt, um entweder invariante Zeitzählimpulse ITCP (mit Perioden tscan) oder variable Zeitzählimpulse VTCP (mit Perioden t.vscan) zu produzieren. In letzterem Fall werden die VTCP's entsprechend der relativen Geschwindigkeit vm (via STQ(v)- Parameter) moduliert, und weisen daher entsprechend kürzere Intervalle auf (siehe dazu Fig. 3b und 3c). Das STQ(v)- Quantum wird von der Abweichung des jeweiligen Start-Potentiales in bezug auf das niedrigste Ruhepotential bestimmt, das als "Referenzwert" dient, und wird durch die Dauer der kapazitiven Ladung einer Zell-Membran gemessen, sobald ein Reiz am Rezeptor auftritt. Diese Ladedauer ist umgekehrt proportional zur Geschwindigkeit des Na+ Einstromes durch die Membran-Kanäle in den intra-zellularen Raum. Eine Zellmembran kann als elektrischer Kondensator betrachtet werden, in dem zwei leitende Medien (die intrazelluläre und die extrazelluläre Lösung) durch eine dünne Isolationsschicht, die Membran, voneinander getrennt sind. Beide Medien bestehen aus verschiedenen Arten von Na/K/Cl- Ionen- verteilungen. Je höher die "Stimulus-Dynamik" (siehe unten) ist, welche zuerst das äußere molekulare Medium beeinflusst - das dem Sensor 2 in Abb. 2a entspricht -, und dann das innere molekulare Medium - das dem Sensor 1 entspricht -, desto schneller ist der Na+Einstrom und desto kürzer ist die Ladedauer (welche die Parameter für die Relativ- geschwindigkeit vm bestimmt) und desto höher die AP- Fortpflanzungsgeschwindigkeit v(ap) in den benachbarten Membran-Distrikten. Die Signalverläufe an der äußeren und der inneren Seite (bzw.der Membran) entsprechen quasi den Signalamplituden V und W. Die Geschwindig- keit v(ap) generiert also indirekt die beschriebenen invarianten Zeitzählimpulse ITCP oder die variablen vm-proportionalen Zeitzählimpulse VTCP. Die besagten variablen VTCP-Impulse sind selbst-adaptiv modulierte Zeitimpulse mit Korre- lation zur relativ zurückgelegten Distanz. Wie im folgenden Abschnitt erklärt wird, existiert (im Gegensatz zu traditionellem physikalischen Verständnis) keine invariante Zeit - nur "wahr- genommene Zeit" ist tatsächlich existent. Von wesentlicher Wichtigkeit ist auch der Unter- schied zwischen "Reiz-Intensität", deren Maß von der AP-Frequenz und somit durch die Refraktär-Phase bestimmt wird, und der "Reiz-Dynamik", deren Maß durch die Ladedauer der kapazitiven Zell-Membran - und deshalb von der Geschwindigkeit des Na+ Zustromes - definiert wird. "Reiz- Dynamik" ist nicht gleichzusetzen mit "Reiz-Intensitätszunahme". Es ist ein Maß für die räumlich/zeitliche Abweichung der relativen Position des Rezeptors in bezug auf die Position der Stimulus-Quelle, und deshalb für die relative Geschwindigkeit vm. " Reiz- Intensität" steht für jene Signalamplituden, aus denen vm-adaptive STQ(d)-Verstreichzeiten Td(1,2,3..) abgeleitet werden, während "Reiz-Dynamik" durch die erfassten STQ(v)- Parametern definiert wird. Fig. 4b und Fig. 4c zeigen die Analyse von STQ-Verstreichzeiten in einem molekular/ biologischen Modell in leicht verständlicher Weise. Die Ergebnisse der Analyse werden dazu benutzt, um redundanzfreie auto-adaptive Muster-Erkennung sowie autonome Regelungs- und Selbstorganisations-Prozesse zu generieren. Im gezeigten Beispiel sollte ein Organismus in die Lage versetzt werden, bestimmte Arten von Fremdkörper, die auf eine Hautpartie drücken, voneinander zu unterscheiden. Er soll mit einem schnellen Muskel-Reflex antworten, wenn er einen Nadelstich als solchen erkennt. Hingegen sollte er den Reiz ignorieren, wenn es sich um einen stumpfen Gegenstand handelt. Dazu ist eine fortgesetzte vm-adaptive Erfassung von STQ(d)-Verstreichzeiten mittels VTCP-Impulse notwendig. Die Frequenz dieser Zeitzählimpulse wird entsprechend den STQ(v)- Parametern aus der Reiz-Dynamik (vm) moduliert. Diese STQ(v)- Parameter werden zur Registrierung der STQ(d)-Verstreichzeiten Td(1,2,3...) aus der Signal-Amplitude der gegenwärtigen Reiz-Intensität benötigt. Der Unter- schied zwischen "Reizintensität" und "Reizdynamik" ist in diesem Beispiel leicht zu verstehen. Ein Stimulus kann verschiedene Intensität auch dann aufweisen, wenn keine zeitlich/räumliche Änderung zwischen Signalquelle und Rezeptor stattfindet. Eine Nadel in der Haut kann auch bei unveränderter Position ein unterschiedliches Empfindungsmuster bewirken, beispielsweise wenn sie erwärmt wird. Dieses Empfindungsmuster wird von der Signalamplitude und somit von der AP-Frequenz und den STQ(d)-Quanten bestimmt. Befindet sich die Nadel in einer invarianten Position, so ist die AP-Fortleitungsgeschwindigkeit konstant, da auch die Membranladezeit konstant ist. Während des Stiches in die Haut ereignet sich ein "dynamischer Reiz", und die STQ(d)-Quantisierung der Signalamplitude geschieht in Abhängigkeit vom Verlauf der Einstichgeschwindigkeit vm. Man beachte, daß während dieses dynamischen Prozesses immer 2 zeitlich verschobene Signal-Amplituden (an der äußeren und der inneren Membranseite) existieren. Die beschriebenen STQ(v)-Parameter leiten von ihnen her. Dem- entsprechend werden die Geschwindigkeiten der AP- Fortpflanzung und die erworbenen STQ(d)- Zeitmuster angepasst ("zeitliche Auto- Adaption"). Diese entsprechend zu vm adaptiv gemessenen STQ(d)-Zeitmuster Td(1,2,3...) werden ständig mit vorausgehend gemessenen und gespeicherten STQ(d)- Zeitmustern Td'(1,2,3...) verglichen und zusammen ausgewertet. Dieser Zeitvergleichs-Prozess geschieht fortgesetzt in den sogenannten "Synapsen", welche die Verbindungsstellen zu axionalen Endigungen anderer Neuronen bilden. Die Wahrscheinlichkeitdichte-Werte, die in den Synapsen ermittelt werden, und die für eine Konvergenz beider Regressions-Kurven stehen, werden zur weiteren Verarbeitung zu peripheren neuronalen Systemen, oder auch an Muskelfasern weitergeleitet, um motorischen Reflex hervorzurufen. Fig. 4b zeigt die vm- abhängige Fortpflanzung eines AP von einem Sensor-Neuron (Rezeptor) 20 entlang eines Neuronenfortsatzes (Axon) zu einer Synapse, wo ein Vergleich mit erworbe- nen Zeit-Sequenzen mittels molekularer "Kovarianzanalyse" stattfindet. Dieser Rezeptor funk- tioniert wie ein "Druck-Sensor". Wenn eine Nadel 21 mit einer bestimmten Dynamik auf die äußere Schicht der Zell-Membran trifft, dann verursacht diese Stimulation das Auslösen von AP's 23, wie in Abb. 4a beschrieben. Die AP's pflanzen sich im Axon 22 mit einer STQ(v)- abhängigen Geschwindigkeit vap fort. Ihre Reihenfolge (a'....v ') entspricht jenem Signal- amplitudenverlauf, der vom Stich hervorgebracht wird. Die Reihenfolge fängt mit dem Phasen- durchgang beim ersten Schwellwert P1 an, geht weiter über P2, P3, P4 (an deren Stelle das Reizmaximum erreicht wird), und kommt schließlich zu den Phasendurchgängen P3 und P2. Die Intensitätsbereiche der Reizwahrnehmung sind mit Z1, Z2, Z3 und Z4 bezeichnet. Die Perioden t(P1), t(P2), t(P3), t(P4).... und die Magnituden der AP's dienen zur Identifikation der jeweiligen Schwelle, wo die Reizintensität sich gegenwärtig befindet. Ihre zeitliche Reihen- folge ist deshalb eine Art von "Code". AP's sind keine Zeitzählimpulse. Neben ihrer Code- Funktion sind sie aber auch (indirekt) Startimpulse und Stopimpulse für die Registrierung von STQ(d)- Verstreichzeiten. Die eigentliche vm-abhängige Messung der STQ-Verstreichzeiten Td(1), Td(2), Td(3), Tw(4) und Td(4)..(s. Abb. 2c), sowie ihr Vergleich mit vorausgehend erfassten Verstreichzeiten findet in der Synapse 24 statt. Am präsynaptischen Ende des Axons laufen die AP 's 23 mit variablen Geschwindigkeiten vm(n ...) ein, die in Relation zur Dynamik des Nadel-Stiches sowie zu den gemessenen STQ(v)- Parametern stehen. Diese variablen Einstrom-Geschwindigkeiten an den Synapsen sind der Schlüssel zum Produzieren jener adaptiven Zeitzählimpulse VTCP (s.Fig. 3c) mit der vm- modulierten Frequenz ƒscan. Die Synapse ist durch den "synaptischen Spalt" von der post- synaptischen Membran getrennt; diese wiederum ist mit anderen Neuronen verbunden, z. B. mit einem sogenannten "Motoneuron" 25. Ein solches Neuron produziert ein sogenanntes "exzitatorisches postsynaptisches Potential" (ESPS) 27, das etwa proportional zur Wahr- scheinlichkeit g einer Konvergenz ist. Wenn dieses EPSP (bzw. die Wahrscheinlichkeitsdichte g) einen bestimmten Schwellwert übersteigt, dann wird erneut ein Aktionspotential AP 28 ausgelöst.Dieses AP wird über Motoaxon 26 zu einer sogenannten "neuromuskulären Endplatte" weitergeleitet, die dort den Muskelreflex verursacht. Die einlaufenden AP- Sequenzen 23 bewirken die Freisetzung bestimmter Quanten von molekularem Transmitter- stoff aus ihren Depots - winzigen kugelförmigen Strukturen in der Synapse, "Vesikel" genannt. Im Prinzip stellt eine Synapse einen komplexen programmierbaren Zeitdatenprozessor und -Analysator dar, der immer dann den Inhalt jeweils eines Vesikels in den präsynaptischen Spalt entleert, wenn das Wiederauftreten irgendeiner früher registrierten synaptischen Struktur innerhalb einer neu registrierten Schlüssel-Struktur bestätigt wird. Die synaptischen Struktur innerhalb einer neu registrierten Schlüssel-Struktur Strukturen und Vesikel- Bewegungen werden von der Dynamik v(ap) des AP-Ioneneinstroms sowie seiner Frequenz erzeugt. AP-Einstromgeschwindigkeiten v(ap) entsprechen den STQ(v)- Parametern, die AP-Frequenzen den STQ(d)-Verstreichzeiten. Die Transmitter-Substanz wird durch die Synapse reabsorbiert und wiederverwertet, sodaß der Zyklus nicht unterbrochen wird. Hier eine ausführliche Beschreibung von Fig. 4b unter Bezugnahme auf Fig. 4e und Fig. 4f: Der Ionen-Einstrom vom ersten einlaufenden AP 23 (a') aktiviert zunächst die Ansammlung von ACh-Transmittermolekülen in den kugelförmigen Strukturen (Vesikeln). Die Dauer dieser ACh-Ansammlung hängt ab von der Dynamik (= Geschwindigkeit vap) des AP-Ionen- Einstromes an der präsynaptischen Endigung und somit auch der Reiz-Dynamik (= vm) am Rezeptor 20. Die Freisetzung der Moleküle in den synaptischen Spalt erfolgt in Form von "Paketen". Jedes nacheinander einlaufende AP - bezeichnet mit b', c'..- bewirkt eine erneute Ansammlung von Neurotransmitterstoffen in Vesikeln, die sich nach erfolgter Auffüllung in Richtung des synaptischen Spalts be- wegen. Alles Folgende hat verstreichzeit-messende und -analysierende Eigenschaften: Die Dauer der Auffüllung mit Transmittersubstanz T(t), die Geschwindigkeiten v(t), mit dem sich die Vesikel in Richtung des synaptischen Spalts weiter- bewegen, ihre Einwirkung auf das synaptische Gitter am Spalt und ihre Positionen, die Öffnungsdauer der Poren usw. Durch diese AP-Einwirkung auf die synaptischen Strukturen werden nicht nur die eigentlichen Zeitzählfrequenzen ƒscan generiert (zur vm-abhängigen Messung jener in Abb. 2c beschriebenen STQ(d)-Versteichzeiten), sondern es werden auch Zeitmuster gespeichert und analysiert. Wenn von der Synapse das Muster eines aktuellen zeitlichen Ablaufes erkannt wird, das mit einer bestehenden gespeicherten Struktur überein- stimmt, dann öffnet sich eine Pore beim synaptischen Gitter, und der ganze molekulare Inhalt eines Vesikels wird in die subsynaptischen Spalt freigesetzt. Die freigesetzten Transmitter- Moleküle (zumeist ACh) binden sich an der anderen Seite des Spalts an spezifische Rezeptormoleküle auf der subsynaptischen Membran des angekoppelten Neurons. Dadurch wird dort ein postsynaptisches Potential (EPSP) hervorgerufen, das sich dann an andere Synapsen, Dendriten oder an eine sogenannte "neuromuskuläre Endplatte" fortpflanzt. Überschreitet das EPSP eine bestimmte Amplitude, dann löst es ein Aktionspotential (AP) der bereits beschriebenen Art aus, das dann z.B. einen Muskel-Reflex hervorruft. Erreicht es diesen Schwellwert nicht, so wird es ähnlich weitergeleitet wie ein EP (also in elektrotonischer Weise); ein AP wird in diesem Fall nicht produziert. Von besonderer Bedeutung ist die addierende Eigenschaft der subsynaptischen Membran. Diese Eigenschaft - auch als "zeitliche Bahnung" bezeichnet - resultiert aus der Summierung der erzeugten EPSP's, wenn diese in kurzer Folge innerhalb bestimmter Zeitfenster eintreffen. Jede Freisetzung von Transmittermoleküle in den synaptischen Spalt zeigt das Auftreten einer erhöhten Wahrscheinlichkeits- Dichte während des Vergleiches aktueller vm-proportional erfaßter STQ-Verstreichzeitmuster mit früheren vm-proportional erfaßten und gespeicherten Zeitmustern an. Erhöhte Wahrscheinlichkeits-Dichte verursacht eine höhere Häufigkeit von Transmittersubstanz- Freisetzung und demnach höhere Summenwerte von EPSP's, was wiederum als Folge eine signifikant höhere Rate von postsynaptischen Aktionspotentialen (AP) produziert. Demnach ist ein postsynaptische AP ein Bestätigungssignal, das anzeigt, dass Isomorphismus zwischen einem früheren und einem aktuell registrierten Zeitdatenmuster erkannt worden ist. Auf der Basis dieses Zeitmuster-Vergleiches wird somit jener Gegenstand, der die Wahrnehmung bei der Rezeptor-Zelle verursacht hatte, als "Nadel" identifiziert; und der Befehl: "Muskelreflex auslösen" wird an die korrespondierenden Muskelfasern weitergeleitet. Parallele komplexere Erkennungsprozesse laufen über das zentrale Nervensystem ZNS (dem Gehirn) ab. Vom beschriebenen druckempfindlichen Hautrezeptor-Neuron 20 gelangt eine weitere axonale Verzweigung 29 über eine Synapse 30 zu einem "ZNS-Neuron". Im Unter- schied zum "Motoneuron", das direkt die motorische Aktivität des Organismus steuert, dient ein ZNS-Neuron der bewussten Erkennung eines rezeptorischen Reizverlaufes. Ein AP 31, das an der postsynaptischen Zellmembran 30 produziert wird, kann auch entlang Dendriten in ein Axon 30a münden, und sich zu mehreren anderen ZNS-Neuronen verzweigen; es kann aber auch indirekt über ZNS-Neuronen zu einem Motoneuron und dann zu einer "neuromusculären Endplatte" gelangen. Die Parameter, welche die Registrierung von STQ-Zeitquanten in den Synapsen 25 und 30 kontrollieren, können sich durch die Verschiedenheit der synaptischen Strukturen unter- scheiden. (Tatsächlich werden ja diese Strukturen von fortgesetzten "Lern"-Prozessen erzeugt). Dies erklärt, warum es möglich ist, dass ein Nadelstich zwar im Gehirn als solcher registriert wird, aber keinen Muskel-Reflex hervorruft; oder aber ein schneller Muskel-Reflex entstehen kann, dessen Ursache durch das Gehirn kaum wahrgenommen wird. Der eine Fall zeigt einen bewussten Reflex, der andere Fall einen instinktiver Reflex. Letzterer tritt auf, wenn die ZNS-Synapse 30 nicht genügend isomorphe Strukturen findet (im Gegensatz zur Synapse 25), daher keine ausreichend häufige Freisetzung von Transmittermolekülen erfolgt, und infolgedessen auch kein postsynaptisches AP 31 und keine bewusste Erkennung des wahrgenommenen Reizes stattfinden kann.Viele Funktionen des zentralen Nervensystemes können so auf monistischer Grundlage erklärt werden; sogar Phänomene wie "Bewusstsein" und "Unterbewusstsein". Im allgemeinen sind auto-adaptive Prozesse in Organismen vielseitig vernetzt und deshalb äußerst komplex. Um fähig zu sein, auf der Haut einen Nadelstich vom Drücken mit einem stumpfen Radierstift zu unterscheiden, sind wesentlich mehr Zeitmuster notwendig; auch müssen mehr Rezeptoren und Synapsen in den Erkennungsprozess einbezogen werden. Fig. 4c zeigt einen Prozess, bei dem das leichte Drücken mit einem stumpfen Gegenstand (z.B. einem konischen Radiergummi auf einem Stift) erkannt wird - wo aber daraus kein Muskelreflex resultiert. Der stumpfe Gegenstand 32 presst mit einer bestimmten relativen Geschwindigkeit vm auf eine Reihe von Rezeptoren in den neuronalen Hautzellen 33, 34, 35, 36 und 37. Aus der Stimulierung der einzelnen benachbarten Rezeptoren (s. auch Fig. 4b) resultieren verschiedene Sequenzen von AP's 39, 40, 41, 42 und 43. Diese Aktionspotentiale pflanzen sich entlang den kollateralen Axonen 38 mit variablen Perioden t(P1,2,3.....) und Geschwindigkeiten vap(1...5) fort, die einerseits von der gegenwärtigen Reizintensität, anderseits von der jeweiligen Reizdynamik abhängig sind. Da jeder Rezeptor-Reiz ein anderes Muster aus STQ(v) und STQ(d)- Quanten erzeugt, ergeben sich für jedes Axon verschiedene AP-Sequenzen a'....m'. Alle einzelnen Sequenzen zusammen stellen jenes Muster aus STQ- Verstreichzeiten dar, das für den Druck mit dem Radierer auf der Haut charakteristisch ist. Diese variablen AP-Ionenströme gelangen zu den Synapsen 44, 45, 46, 47 und 48, welche über den synaptischen Spalt mit dem Motoneuron 49 verbunden sind. Sobald das aktuell erfasste Zeitdatenmuster eine Ähnlichkeit zu einem früher erfassten Zeitdatenmuster auf- weist, setzt jede einzelne Synapse den Inhalt eines Vesikels in den subsynaptischen Spalt frei. Gleichzeitig produziert diese Freisetzung ein ESPS an der subsynaptischen Membran des Neurons. Diese Potentiale sind zumeist unterschwellig. Der nötige Schwellwert für die Auslösung eines AP wird nur dann erreicht, wenn mehrere EPSP's summiert werden. Dies geschieht nur dann, wenn eine sogenannte "zeitliche Bahnung" solcher Potentiale stattfindet, wie im Abschnitt zuvor beschriebenen wurde. Im gezeigten Modell wirken sich diese addierenden Eigenschaften auf die einzelnen ESPS's 50, 51, 52, 53 und 54 aus. Diese Potentiale entsprechen den rezeptor-spezifischen Wahrscheinlichkeitsdichte-Parametern g1, g2. g3, g4 und g5, die für den jeweilige Grad an Isomorphität von Zeitmustern stehen. Gleichzeitige Transmitterfreisetzung in mehreren Synapsen (z.B. in 45 und 47) bewirkt die Addierung der einzelnen EPSP's zu einem Gesamt- Potential 56, das der Summe der einzelnen Wahrscheinlichkeitsdichten (G) = (g1+ g3) entspricht. Diese Eigenschaft der Neuronen, räumlich getrennte unterschwellige EPSP 's zu summieren, wenn gleichzeitige Transmitter-Freisetzung bei einer Anzahl paralleler Synapsen auf der selben subsynaptischen Membran auftritt, bezeichnet man als "räumliche Bahnung". Im beschriebenen Modellfall erreicht das summierte EPSP 56 aber nicht die bezeichnete Schwelle (gt) und es wird daher kein AP ausgelöst. Statt dessen pflanzt es sich im subsynap- tischen Membrandistrikt 49 des Neurons bzw. im nachfolgenden Motoaxon 55 als passives elektrotonisches Potential (EP) fort. Ein solches EP schwächt sich (zum Unterschied von einem selbst-regenerierenden aktiven AP) nach wenigen Millimetern im Axon soweit ab, dass es keinerlei aktivierenden Einfluss auf die neuromuskuläre Endplatte hat, und somit auch keinen aktivierenden Einfluss auf den Muskel. Die Reizung der Haut und das Anpressen mit dem Radierstift reicht also nicht aus, um einen Muskelreflex hervorzurufen. Anders wäre es der Fall, würde der Radiergummi abbrechen und der leere Stift mit voller Wucht auf die Haut- Rezeptoren treffen. In diesem Fall würde eine Transmitterfreisetzung gleichzeitig in allen fünf Synapsen 50, 51, 52, 53 und 54 ausgelöst, weil die erfassten STQ-Zeitmuster Td(1,2,3....) mit sehr hoher Wahrscheinlichkeit ähnlich mit jenen in den synaptischen Strukturen gespei- cherten STQ-Zeitmustern Td'(1,2,3..) wären, die für das Ereignis "Nadelstich" signifikant sind. Die EPSP 's würden wegen der Eigenschaft ihrer zeitlichen und räumlichen "Bahnung" zu einem überschwelligen EPSP 56 addiert werden und ein post-synaptisches AP hervorrufen, das sich im Motoaxon 55 in einer selbst-regenerierenden Weise (ohne zeitliche und räumliche Abschwächung) bis zum Muskel fortpflanzen würde um einen Muskel-Reflex zu produzieren. Wie in Fig. 4b, so kommt es auch im vorliegenden Beispiel zu einem parallel verlaufenden Erkennungsprozess, der im zentralen Nervensystem (ZNS) stattfindet. Von den Hautrezeptor- Zellen 33, 34, 35, 36 und 37 gelangen kollaterale axonale Verzweigungen 57 zu ZNS- Synapsen, die an andere Neuronen 58 gekoppelt sind. Solche Verzweigungen werden als "Divergenzen" bezeichnet. Die Aufsplitterung der Axone in kollaterale Verzweigungen zu verschiedenen neuronalen ZNS-Distrikten, und die zeitliche und räumliche Kombination vieler postsynaptischer EPSP's ermöglicht die bewusste Erkennung komplexer Wahrnehmungen im Gehirn (z.B. die Tatsache, dass ein Radierstift auf die Haut drückt). Da diese Erkennung unabhängig von der Auslösung eines etwaigen Muskelreflexes stattzufinden hat, muss die Summe einzelner ESPS's im ZNS auf jeden Fall überschwellig sein. Ansonsten könnte kein postsynaptisches AP - und somit auch kein Bestätigungssignal produziert werden. Als wesentliche Vorbedingung dazu ist notwendig, daß auto-adaptive Prozesse vorangingen, wodurch bestimmte präsynaptische und subsynaptische STQ-Zeitstrukturen in den parallelen Synapsen 58 geprägt wurden. Diese Strukturen enthalten Information (Zeitsequenzen, Zeitmuster..), die für ähnliche Sinnes-Erfahrungen stehen (z. B. in die Haut eindringende Gegen- stände, darunter auch der besagte Radierstift). Offensichtlich hat die Schwelle für das Verursachen eines AP's in der postsynaptischen Membran-Struktur der ZNS-Neuronen 58, (und deshalb auch im Gehirn) niedriger zu sein als beim vorher beschriebenen Motoneuron 49. Daher muss auch die Summe dieser ESPS's größer sein als diejenige der ESPS's g1, g2, g3, g4 und g5. Isomorphitäten von STQ-Zeitdatenreihen in den ZNS-Synapsen des Gehirns haben demnach ausgeprägter zu sein als jene in den Synapsen von Motoneuronen, die nur für Muskelreflexe zuständig sind. Die Strukturen von ZNS-Synapsen müssen Informationen besser unterscheiden können, und somit subtiler beschaffen sein. Das Auftreten eines sub- synaptischen AP stellt eine Bestätigung für die Tatsache dar, dass ein aktuell erfasstes Td(1,2,3...)- Zeitmuster in virtueller Weise isomorph ist mit einem früher registrierten Td'(1,2,3...)- Referenzzeitmuster, das z.B. aus einer älteren Sinneserfahrung mit einem an irgendeine Hautstelle drückenden Radierstift stammt. Hat eine solche frühere Erfahrung nicht stattgefunden, so hat das Bewusstsein keine physikalische Grundlage zur Erkennung, da die Zeitmuster-Vergleichsbasis fehlt. In einem solchen Fall hätte also zunächst ein Lernprozess vorauszugehen. Meistens werden dazu auch andere, aus verschiedenen Rezeptorreiz- Ereignissen hergeleitete Empfindungserfahrungen visueller oder akustischer Art usw. mit der erwähnten Druckempfindungs-Erfahrung koordiniert. Dies erklärt, warum ZNS-Strukturen äußerst umfangreich vernetzt sind. ZNS-Neurone, aber auch Motoneurone, besitzen bis zu 5000 angekoppelte Synapsen, die in verschiedenster Weise mit Rezeptor- Neuronen und axonalen Verzeigungen verknüpft sind. Es existieren komplexe Zeitdaten-Muster für niedrigere und höhere Aufgabengebiete, die in hierarchischer Weise strukturiert sind. Einfache Td(1,2,3...) und Td'(1,2,3...)- Analyse-Operationen wurden bereits beschrieben. Kreislauf, Atmung, Koordination von Muskelsystemen, Wachstum, Sehen, Hören, Sprechen, Riechen usw. erfordern eine enorme Anzahl synaptisch registrierter "Land- schaften" von STQ-Zeitmustern im Organismus, die von vielen Rezeptoren produziert wurden; und welche fortgesetzt auf Isomorphität mit aktuell aufgenommenen STQ-Zeitmustern analysiert werden müssen. Dementsprechend ereignet sich zeitliche und motorische Auto-Adaption in tieferen und höheren Hierarchien und auf verschiedenen Niveaus. Fig. 4d zeigt das Gegenstück zu einem EPSP (erregendes postsynaptisches Potential); das "inhibitorische postsynaptische Potential", oder IPSP. Wie aus der Zeichnung zu sehen ist, sind die IPSP- Potentiale 61, 62, 63, 64 und 65 an der subsynaptischen Membran 60 im Unterschied zu besagten EPSP's negativ. IPSP's werden von einem erheblichen Teil der Synapsen produziert, um präsynaptische Hemmung statt Aktivierung hervorzurufen. Das Beispiel zeigt hier ein sich vom Motoaxon 66 zu einer neuomuskulären Endplatte (beziehungs- weise Muskelfaser) fortpflanzendes Summen-IPSP 67, welches verhindert, dass dieser Muskel aktiviert werden kann - selbst dann nicht, wenn ein überschwelliges EPSP zur gleichen Zeit über ein paralleles Motoaxon die gleiche Muskelfaser erreichen würde. Positive EPSP's-Ionenströme und negative IPSP's-Ionenströme heben sich gegenseitig auf. Die hauptsächliche Funktion von IPSP's besteht darin, koordinierte und homogene Zustands- veränderungen im Organismus, z.B. exaktes Timing von Bewegungsvorgängen zu ermöglichen. Um beispielsweise einen gleichmäßigen Armschwung durchzuführen, ist es erforderlich, den Musculus biceps, der den Ellenbogen beugt, mittels EPSP's zu aktivieren; gleichzeitig aber den antagonistischen Musculus triceps (der den Ellenbogen streckt), mittels IPSP's zu hemmen. Antagonistische Muskel müssen über sogenannte "antagonistische Motoneuronen" gehemmt werden, während der andere Muskel über "homonyme Motoneuronen" aktiviert wird. Der komplexe Synergismus von erregenden EPSP-Synapsen und hemmenden IPSP-Synapsen wirkt wie ein Feedback-System (Regelkreis) und ermöglicht optimales Timing und Effizienz im Organismus. Man kann diesen Prozess mit einem Servo- Antrieb oder einer Servo- Lenkung vergleichen, welche eine korrekte koordinierte Ausführung momentaner Bewegungsphasen durch datenunterstützte Operation und Regelung ermöglicht. Wenn Daten ausfallen, bricht der Servo-Kreis zusammen. Störungen in einem molekular-biologischen Regelkreis, der durch STQ-Zeitdatenstrukturen gestützt wird, führen zu tetanischen Zuckungen, willkürlichen Kontraktionen, chaotischen Krämpfen usw. Vom kybernetischen Standpunkt betrachtet, erzeugt jede erregende Synapse einen "motori- schen Impuls" (EPSP), jede hemmende Synapse einen "Bremsimpuls" (IPSP). Das stetige Abstimmen der komplizierten Regelkreise, und die Balance, die aus dem fortgesetzten Vergleich von früheren sensorischen Erfahrungen (den gespeicherten referenten Zeitmustern) mit aktuellen sensorischen Erfahrungen (den aktuell erfaßten Zeitdatenmustern) resultiert, erzeugt ein "perfektes Timing" im Organismus. Fig. 4e zeigt die prinzipielle Gestaltung einer Synapse. Das Axon 68 mündet in die prä- synaptische Endigung 69, die auch "Bouton" genannt wird. Die seriell einlaufenden AP's verursachen die Auffüllung der Vesikel mit Neurotransmitter-Mulekülen. Ist der Auffüllprozess beendet, beginnen sich die Vesikel in Richtung präsynaptisches Vesikelgitter 71 zu bewegen. Wenn ein gegenwärtig erworbenes Zeitmuster annähernd isomorph einem bestehenden Zeitmuster ist, (s. auch Fig. 4b), dann öffnet sich bei einer Andockstelle am synaptischen Gitter ein kleiner Kanal, der den ganzen Inhalt des Vesikels in den schmalen synaptischen Spalt 72 freisetzt. Dieser Vorgang wird auch als "Exozytose" bezeichnet. An der subsynaptischen neuronalen Membran 73 befinden sich spezifische molekulare Rezeptoren 73a, an die sich die freigesetzten Transmittermoleküle heften. Für eine bestimmte Dauer wird eine eine Pore geöffnet, durch welche die Transmitter-Substanz diffundiert. Die Leitfähigkeit der postsynaptischen Membran erhöht sich und das besagte EPSP (die darauffolgende postsynaptische Depolarisation) wird ausgelöst. Die Öffnungs-Dauer der Poren und die Erkennung komplementärer Rezeptoren durch die Moleküle wird gleichfalls von auto-adaptiven Prozessen und Evaluationen von STQ-Zeitmusterstrukturen bestimmt. Allerdings stellen diese Prozesse Subphänomene von niedrigerer Stufe im Vergleich zu synaptischen Phänomenen dar. Strukturen zur zeitlichen und motorischen Auto-Adaption, die auf der Quantisierung von STQ-Verstreichzeiten beruhen, existieren auch auf molekularem und atomarem Niveau. Fig. 4f zeigt das Auffüllen eines Vesikels 70 mit Transmitterstoffen und seine darauf folgende Bewegung zu einem präsynaptischen Andockvorsprung am Vesikelgitter 71. Der Beginn der Auffüllung 74 ist mit der Aktivierung einer Stoppuhr vergleichbar. Das Tempo v(t) der Vesikel- Auffüllung ist proportional zur Dynamik des AP-Ioneneinstroms vap in die Synapse. Die Perioden der Auffüllungen T(t...) richten sich nach den Perioden t(P1,P2...) der eintreffenden AP's; somit stellen diese Zeiten quasi vm-adaptiv quantisierte STQ(d)- Verstreichzeiten Td(1,2,3...) usw. dar. Die Vesikel- Bewegungsrichtung ist mit 75 bezeichnet. Wenn das aktuelle Tempo v(t), die Dauer der Vesikel-Auffüllung T(t), die Transmitter-Menge, die aktuelle Vesikel-Bewegung und andere aktuelle signifikante STQ-Parameter korrelative Eigenschaften zu bestehenden synaptischen STQ-Strukturen haben, so heftet sich ein aufgefüll- tes Vesikel an einen Andockvorsprung 77 am Gitter. Ca++ Ionen strömen in die Synapse ein, eine Pore am kristallinen Vesikelgitter öffnet sich, und der gesamte molekulare Transmitter- inhalt entleert sich in den synaptischen Spalt 72. An der postsynaptischen Membran der Ziel-Zelle fusionieren sich diese Moleküle mit den spezifischen Rezeptor-Molekülen. Diese Rezeptoren haben Verifizierungs-Aufgaben. Sie verhindern, dass fremde Transmitterstoffe (die aus anderen Synapsen stammen) an diesem Neuron falsche ESPS's auslösen könnten. Zur Vervollständigung dieses Kapitels werden die Beschreibungen zu Fig. 4a, 4b, 4e und 4f in Kontext zu den STQ-Konfigurationen von Fig. 3c - 3g gebracht. Als Argumentationsbeispiel wird wieder angenommen, dass ein Nadelstich auf eine Rezeptor-Zelle trifft (s. auch Fig. 4b): Jene IP-Sequenzen, die in Fig. 3a gezeigt werden, entsprechen den AP's 23, die durch das Stimulieren einer Rezeptorzelle 20 mit einer Nadel 21 produziert werden. Ihre Perioden t(P1), t(P2) ... dienen der Zuordnung der jeweiligen Zone der Reizintensität (P1, P2...) oder der Wahrnehmungsintensität (Z1, Z2..). Jedes in einer Synapse 69 einlaufende AP löst eine von seiner axonalen Fortleitungsgeschwindigkeit (vap)-abhängige adaptive Quantisierung von STQ(d)-Verstreichzeiten aus. Die Verstreichzeitnahme mit modulierter Zeitbasis wird ausgelöst, sobald eine Vesikel-Auffüllung beginnt. Eine beendete Auffüllung bedeutet "Verstreichzeitnahme gestoppt; STQ(d)-Quantum registriert". Diese solcherweise registrierten Verstreichzeiten Td(1), Td(2), Td(3), Td(4)...usw. generieren die signifikanten synaptischen Strukturen. Invariante Zeitzählimpulse ITCP (s. Fig. 3b) mit der Frequenz fscan entsprechen einer konstanten axonalen AP-Fortpflanzung mit der Geschwindigkeit vap, wenn kein dynamischer Stimulus der besagten Hautrezeptor-Zelle gegeben ist; (z.B. wenn eine Nadel in einer fixen Position verharrt und eine konstante Reizintensität erzeugt). In diesem Fall erfühlt die Rezeptor-Membran keine relative Geschwindigkeit vm, die AP 's pflanzen sich mit fixem vap entlang dem Axon 22 fort; und die Synapse quantisiert die STQ(d)-Verstreichzeiten mit invarianter Zeitzählfrequenz fscan. Jene Zeitzählimpulse VTCP (s. Fig. 3c) mit der variablen Frequenz ƒscan kommen dann zur Anwendung, wenn ein dynamischer Reizverlauf auf den Rezeptor einwirkt. Moduliert nach der jeweiligen variablen Dynamik vm(n...), welche als STQ(v)-Parameter von der Membran gemessen wird, pflanzen sich die AP's entlang des Axons mit STQ(v)-proportionaler Geschwindigkeit vap(n..) fort. In gleicher Weise, wie in der Beschreibung zu Fig. 3c die adaptive Anpassung der Zeitzählfrequenzen zu den Übergängen 2.1, 3.1, 4.1... dargelegt wurde, so ändern sich hier die AP-Ioneneinstrom-Geschwindigkeiten v(t....) an der Synapse, die Vesikel-Auffüllzeiten T(t...), die Quantität der Transmittermoleküle in Vesikeln, ihre Bewegung in Richtung Vesikel-Gitter, die Struktur dieses Gitters und viele andere Parameter der präsynaptischen und subsynaptischen Strukturen. Eine Synapse besitzt Eigenschaften, die es ermöglichen, die Dynamik der einströmenden AP's in vap-proportionale molekulare Zustandsveränderungen umzusetzen. Diese wirken so, wie variable VTCP-Zeitzählimpulse in Fig. 3c. Der Prozess kann verglichen werden mit variablem Wasserdruck, der eine Turbine antreibt, durch welche ein Generator variable Frequenzen er- zeugt, die vom Druck und vom Tempo des Wassers abhängen: erhöhter Wasserdruck steht für höhere Reizdynamik am Rezeptor, für höhere axonale AP-Fortleitungsgeschwindigkeit vap, und für höhere VTCP-Zeitzählfrequenz ƒscan in der Synapse (die sich nicht nur auf das Tempo v(t) auswirkt, mit dem Vesikel sich auffüllen, sondern auch auf viele andere synaptische Parameter). Entsprechend dieser Prozesse werden die STQ(d)-Sequenzen Td(1,2,3...) usw. in der Synapse mit vm-modulierten Zeittaktfrequenzen ƒscan (1,2,3...) registriert; und als Konsequenz daraus wird von dieser Zeitreihe die physikalische Struktur der Synapse geprägt. Fig. 3d zeigt eine aktuell erfasste Zeitdaten-Reihe 32 30 22 23 20, die äquivalent ist zum registrierten Zeitmuster Td(1,2,3,...), welche in der Synapse 24 eine spezifische moleku- lar/biologische Spur hinterlässt. Die gezeigte früher erfasste Zeitdatenreihe 30 29 22 24 19 in Fig. 3e entspricht jener synaptischen Struktur, die durch oftmalige Reproduzierung bestimmter Stimulus-Ereignisse und Zeitmuster Td'(1,2,3...) "geprägt" worden ist. Die manifestierte synaptische Td'- Struktur kann auch als Fußstapfen-Sequenz betrachtet werden, die durch fortgesetzte Lern-Prozesse und Wahrnehmungs-Erfahrungen erzeugt wurde, und die z.B. als Referenz-Muster für das Ereignis "Nadelstich" dient. Wenn eine neu erworbene Td-Fußstapfensequen - die durch gegenwärtige Charakteristiken der Vesikel- Ansammlung und andere signifikante zeitabhängige Parameter bestimmt wird - ungefähr mit dieser bestehenden T'-Fußstapfenfolge (oder mit einem Teil davon!) Schritt hält, dann wird in der synaptischen Struktur "Kovarianz" erkannt. Dies resultiert in der Öffnung einer Vesikel- Andockstelle am synaptischen Gitter und in der Freisetzung aller in einem Vesikel enthaltenen Transmitter-Moleküle, worauf ein EPSP an der sub-synaptischen Membran 25 produziert wird. Das Potential eines EPSP entspricht jenen in Fig. 3f gezeigten Wahrscheinlichkeitsdichte- Parametern, die für die momentan bewertete Kovarianz signifikant sind. Wenn solche Wahrscheinlichkeitsdichte-Parameter sich innerhalb eines bestimmten Zeitintervalls zu einem bestimmten Schwellwert-Potential 27 addieren, wird ein AP 26 produziert. Dieses AP dient als Bestätigung für das Ereignis " Nadel erkannt", und ruft einen Muskel-Reflex hervor. Der Vergleich aktueller Verstreichzeitmuster mit früher erfassten Verstreichzeitmustern, wie er in Fig. 3g gezeigt wird, findet in der Synapse fortgesetzt statt. Jede erkannte Kovarianz einer neuen Zeitsequenz, die durch besagte "zeitliche Auto-Adaption" registriert wird, setzt eine Art von "Andock-Mechanismus" in Gang. Er initiiert jenen Prozess, der vom Patent- anmelder als "motorische Auto-Adaption" bezeichnet wird, und welcher als der eigentliche "Motor" in biologisch-chemischen Organismen bzw. Lebensformen verstanden werden kann. Strukturen zeitlicher und motorischer Autoadaption, die auf STQ-Quantisierung beruhen, existieren auch auf unterster molekularer Ebene. Ohne verstreichzeit-gestützte molekulare Regelkreise wären koordinierte Zustandsveränderungen in biologischen Systemen unmöglich. Dies trifft insbesondere auf Bewegungen von Proteinen, auf die Erkennung und Kopierung des genetischen Codes, und auf andere grundlegende Lebensprozesse zu. Der Schaffung höherer biologisch/chemischer Ordnungen und komplexer Systeme wie Synapsen oder Neurone geht die Existenz einer STQ-quantisierenden molekularen Substruktur voraus, aus der einfache Erkennungs- und Selbstorganisations-Prozesse von niedrigerem Niveau abgeleitet werden. Tatsächlich gibt es unzählige Hierarchien von auto-adaptiven Phänomenen auf verschiede- nen Ebenen. Einfache Phänomene auf molekularer Basis sind z.B. auch: das "Andocken" an Rezeptormolekülen, die Bildung von Poren, Ionenkanälen und subaxonalen Transportstrukturen (Mikrotubuli), und die Formierung neuer Synapsen und axonaler Verzweigungen. Demgegenüber stellt die in der Beschreibung zu Fig. 4a - c gezeigte Erkennung von Reiz- Signalverläufen durch synaptischen Zeitmuster-Vergleich (als vegetativer Reflex oder als bewusste Wahrnehmung) ein Epiphänomen bezüglich dessen dar. Jedes derartige auto-adaptive STQ-Epiphänomen wird seinerseits von höherrangigen STQ- Epiphänomenen überlagert; ein Beispiel dafür ist die Analyse komplexer "Zeitmuster-Landschaften" auf Isomorphität. STQ- Epipänomene wie Regelung des Wachstums, des Kreislaufes, der Körpertemperatur, der Atmung, des Stoffwechsels, des Sehens, des Hörens, des Tastens, des Riechens, der Bewegungskoordination usw. werden ihrerseits wieder von noch komplexeren STQ-Szenarien übertroffen, wozu unter anderem das Bewusstsein, das Denken, der freie Wille, das bewusste Handeln oder auch die bewusste Zeitempfindung des Organismus zählen. In allen diesen Fällen forscht das zentrale Nervensystem nach konvergenten Zeitmustern, die wie einzelne Puzzle-Stücke zu einem integrierten sensorischen Gesamtszenario zusammengesetzt werden. Findet sich in irgendeiner Hierarchie innerhalb einer gewissen "Latenzzeit" trotz intensiver "Suche" für eine Td-Sequenz kein konvergentes Sub-Zeitmuster, so zeigt der Organismus chaotisches Verhalten. Dieses Verhalten beschränkt sich auf jenen Teilbereich, in dem der Kollaps aufgetreten ist. Sobald ein kovariantes Zeitmuster gefunden ist, kehrt der geordnete Prozess der zeitlichen und motorischen Auto-Adaption (und Auto-Emolution) zurück. Dies ist auf triviale Weise mit einer Servolenkung vergleichbar, die kurzfristig ausfällt. Das chaotische Verhalten wird jedoch ebenfalls in seinem Ablauf als STQ-Zeitmuster quantisiert und in den involvierten Synapsen auf eine Weise registriert, dass es trotz einströmender AP's zu keiner Freisetzung von Neurotransmitter-Substanzen kommt. Über subaxonale Transportstrukturen (sog. Mikrotubili) strömen solche Informationen als Transmittermoleküle in inverser Richtung entlang des Axons zurück. Mikrotubili dienen zur Schaffung neuer Synapsen, und zur synap- tischer Anbindungen an solche Neuronen und neuronalen Netze, in denen ebenfalls ein Kol- laps eines Autoadaptionsprozesses aufgetreten ist. Der Produzierung neuer Synapsen geht die Entstehung von Dendriten voraus; das sind axonale Fortsätze, die aus Neuronen hervorsprießen. Auf diese Weise regeneriert sich der auto-adaptive neuronale "Feedback"- Mechanismus von selbst, und jenes STQ-Zeitmuster, das während des kurzfristigen "chaotischen Verhaltens" erfasst wurde, wird zu einer neuen Referenzbasis für künftige Ereignisse. Auf diese Weise lernt der zentrale Nervensystem (ZNS), neue Ereignisse und Erfahrungen zu registrieren; und neue Zeitmuster einzubeziehen, die vorher unbekannt waren. Fig. 5 zeigt eine Konfiguration, in der die beschriebene erfundene Methode angewandt wird, um einen autonomen selbst-organisierenden Mechanismus (insbes. einen Roboter) zu generieren, bei dem die STQ-Quanten mittels mechanistischer Sensor-Technologie und Elektronik-Schaltkreise erworben werden. Im Unterschied zu Fig. 4a - f werden im gezeigten Fall beinahe ausschließlich STQ(i)-Verstreichzeiten zusammen mit STQ(v)- Verstreichzeiten (die für die Messung der relativen Momentangeschwindigkeit benötigt werden) quantisiert. Die mit Tw(1,2,3....n) bezeichneten Zeitdatenströme resultieren aus den vm-adaptiven STQ(i)-Verstreichzeitmessungen. Nichtsdestoweniger wäre es aber vorteilhaft, auch STQ(d)- Quanten zu erfassen, die zur Verifizierung von erworbenen Tw-Zeitdatenströmen dienen können. Im Gegensatz zu molekular/biologische Organismen ist es in mechanistischen Syste- men kaum möglich, eine verhältnismäßig große Anzahl von Sensoren auf engstem Raum neben- einander zu placieren. Daher ist es erforderlich, aus der verfügbaren mechanistischen Sensor- Technologie soviel STQ- Verstreichzeiten als möglich zu gewinnen, um eine ausreichende große Referenzbasis für die nachfolgende statistische Analyse zu erlangen. Wie bereits in der Beschreibung zu Fig. 3a ausgeführt wurde, fallen bei multiplen STQ(i)-Quantisierungen Zeitdaten parallel und gleichzeitig an, weshalb diese Daten auch in paralleler Weise verarbeitet werden müssen.      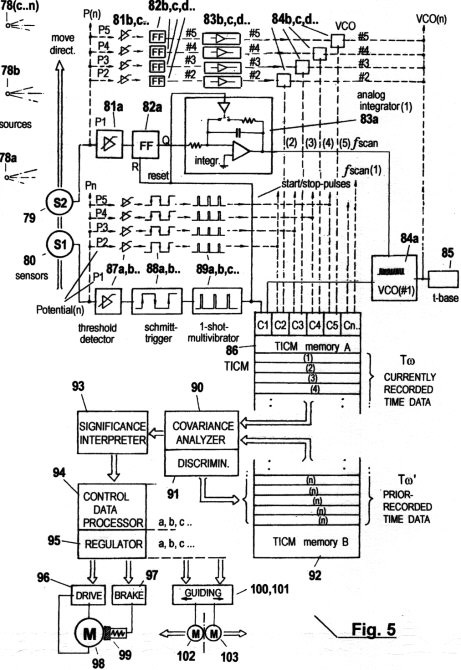Die Konfiguration zeigt ein Blockschaltbild eines mobilen autonomen Roboters mit der angeeigneten Fähigkeit, Bewegungsphasen in auto-adaptiver Weise zu reproduzieren und das Timing seiner Eigenbewegung durch fortgesetztes Abtasten und Erkennen seiner physikalischen Umgebung zu optimieren. Das Robotiksystem ist mit gleichartigen benach- barten Sensoren 79 und 80 bestückt, welche analoge Ausgangssignale liefern, die mit Schwellwertdetektor-IC's 81a, b, c, d ,e.. und 87a, b, c, d, e... verbunden sind. Bewegt sich Sensor 79 (der "V-Sensor") in der bezeichneten Richtung entlang der korrespondieren- den äußeren Signalquelle 78a, so durchbricht dessen Signalamplitude zunächst das niedrigste Potential P1, das vom Schwellwertdetektor 81a bestimmt wird (s. Beschreibung zu Fig. 2b). Dadurch wird das Flip-Flop 82a getriggert (Output = H). Ein Schmitt-Trigger-IC sowie ein Monoflop-IC sollte vorgeschaltet sein, um bei jedem Phasen- durchgang kurze Impulse abzugeben. Der nachgeschaltete rücksetzbare Präzisions- Integrator(1) 83a liefert nun ein stetig ansteigendes analoges Output-Signal, das die Frequenz des programmierbaren Oszillators (VCO) 84a moduliert. Diese Frequenz ist mit dem Input eines digitalen TICM (Vielfach-Zeitzähl- und Speicher-IC) 86(C1) verbunden und bildet die aktuelle vm-adaptive Zeitzählfrequenz ƒscan(1) (s. auch Fig. 3b, 3c). Der Integrator (1) 83a dient demnach zur STQ(v)- Quantisierung. Er misst die Verstreich- zeit Tv(1) in Form eines Potentialanstiegs, der über den VCO(#1) 84a in besagte Zähl- frequenz ƒscan(1) umgewandelt wird, welche anti-proportional zu den relativen Geschwindig- keiten vm(n..) ist, mit der sich das Robotiksystem gegenüber der räumlichen physikalischen Umgebung bewegt. Gelangt der benachbarte Sensor 80 (der "W-Sensor") in den Wahrnehmungsbereich der Signalquelle 78a, so durchbricht seine Signalamplitude zunächst das vom Schwellwert-detektor-IC 87a bestimmte niedrigste Potential P1 (s. Beschreibung zu Fig. 2b). Als Ergebnis produziert die steigende Flanke des anschließenden Schmitt-Trigger-IC 88a einen Impuls im nachgeschalteten Monoflop-IC 89a, der im TICM 86 (C1) die STQ(i)-Quantisierung der vm- adaptierten Verstreichzeit Tw(1) startet. Da gleichzeitig ein Reset-Impuls an das Flip-Flop 82a geht und daher der analoge Pegel am Output des Integrators(1) 83a gehalten wird, verbleibt die Zählfrequenz ƒ(1) als momentane vm-abhängige Zeitzählbasis ƒscan (1) am Output des TICM 86(C1) solange unverändert, bis der nächste STQ(v)-Parameter quantisiert wird. Diese Quantisierung findet statt, wenn die Signalamplitude des Sensors 79 unter das vom Schwellwertdetektor-IC 81a festgelegte Potential P1 fällt (wobei das Flip-Flop 82a von der fallenden Signalflanke getriggert wird), oder wenn der Sensor 79 in den Wahrnehmungs- bereich einer weiteren Signalquelle 78b,c,d,e.. gelangt. Gleichzeitig wird dabei über IC's 87a, 88a und 89a erneut ein Impuls produziert, der die Messung der Verstreichzeit Tw(1) im TICM 86(C1) stoppt und die gezählten vm- modulierten Zeitimpulse im Zeitdatenspeicher (C1) ablegt. Im Memory-Bereich C1 sind jene Tw-Verstreichzeiten gespeichert, die sich auf das niedrigste Potential P1 beziehen, beispiels- weise Tw(1), Tw(8), Tw(15) usw. Die Quantisierung aller auf die höheren Potentiale P2, P3, P4, P5 usw. bezogenen STQ-Verstreichzeiten wird in derselben Weise abgewickelt wie für P1. Passiert die Signalamplitude aus Sensor 79 die von den Detektor-IC's 81b, c, d, e... bestimmten Schwellwert-Potentiale P2, P3, P4, P5.., so triggern nacheinander die Outputs der Flip-Flop's 82b, c, d, e.. auf = H, und die nachgeschalteten Integratoren 83b, c, d, e... liefern stetig ansteigende analoge Output-Pegel, welche ihrerseits die Frequenzen ƒscan (von den VCO's 84b, c, d, e.. produziert) solange stetig vermindern, bis die Signalamplituden aus Sensor 80 die von den Detektor-IC's 87b, c, d, e.. bestimmten höheren Schwellwert- Potentiale P2, P3, P4, P5.. erreichen, sobald dieser Sensor in den Wahrnehmungsbereich der Signalquelle 78a gelangt. Daraufhin werden die Schmitt-Trigger 88b, c, d, e.. aktiviert, und die Monoflops 89b, c, d, e... produzieren Impulse, die im TICM 86(C2,C2,C3,C4 ...Cn) die Erfassung der vm-adaptierten Verstreichzeit-Daten Tw(1,2,3,4....n) starten. Die Registrierung dieser Daten geschieht während die momentanen vm-adaptierten Zeitzählfrequenzen ƒscan (1,2,3,4,..n) gelten, weil die gleichzeitig an die Flip-Flops 82b, c, d, e.. ergangenen Reset-Impulse die Output-Pegel der Integrator-IC's 83b, c, d, e.. halten, womit die entsprechenden Output- Frequenzen ƒ(1,2,3,4...n) an den VCO's 84b, c, d, e...festgelegt werden. In derselben Weise erfolgen die fortgesetzten Quantisierungen weiterer Tw-Verstreichzeiten, wenn sich die Sensoren 79, 80 entlang weiterer Signalquellen 78b, c, d, e... bewegen. Im TICM 86 (C1...n) werden alle quantisierten STQ(i)-Zeitdaten abgelegt. Im Speicherbereich C2 (s. die korrespondierende Fig. 2b) befinden sich die auf den Wahrnehmungs-bereich (Potential) P2 bezogenen Verstreichzeiten Tw(2), Tw(7), Tw(14)..., im Speicherbereich C3 die auf die höhere Potentialstufe P3 bezogenen Verstreichzeiten Tw(3), Tw(6), Tw(13)..., im Speicherbereich C4 die auf die nächsthöhere Potentialstufe P4 bezogenen Verstreichzeiten Tw(4), Tw(5), Tw(12)..usw. Die im TICM 86 einströmenden aktuellen Tw-Sequenzen werden demnach durch die aktuelle Bewegung des sensor-gekoppelten autonomen Mechanismus (z.B. "Roboter-Vehikel") entlang einer bestimmten Bahn generiert. Im gezeigten Beispiel weichen die Positionen der Sensoren bezüglich der Positionen der externen Signalquellen (den physikalischen Umgebungen) zeitlich ab. Im Falle absoluter physikalischer Invarianz zwischen dem autonomen Vehikel und den Umgebungen (auch ident mit "absoluter Synchronität") kann weder ein STQ-Parameter noch eine Tw-Sequenz erworben werden. Tritt keine solche physikalische Invarianz auf, dann ist es für das autonome Vehikel möglich, seine eigene Bewegung entlang der Bahn durch den stetigen Vergleich aktuell erfasster STQ-Zeitdatenmuster Tw(1,2,3..n) mit früher erfassten STQ-Zeitdatenmuster Tw'(nnnn) zu erkennen; und es ist auch möglich die erkannten Bewegungen fortgesetzt in auto-adaptiver Weise zu optimieren. Voraussetzung dafür ist, dass das Vehikel über ein entsprechendes Antriebs- und Bremssystem verfügt, das durch Daten kontrolliert wird, die mittels fortgesetzten statistischen Zeitdaten-Analysen errechnet werden. Man vergleiche dazu auch Fig. 3d und 3e: Sobald die Regressions-Kurve einer aktuellen, im TICM 86 gespeicherten Zeitdaten-Sequenz Tw (1,2,3...), mit der Regressionskurve einer zeitlich zurückliegenden, durch eine frühere gleichartige Bewegung entlang derselben erfassten Zeitdaten-Sequenz Tw'(nnn) konvergiert, wird das Antriebssystem 98 (sowie das Bremssystem 99) durch Impulse 96, 97 aktiviert, die das Vehikel dazu veranlassen, seine Bewegungsverläufe entlang den externen Signalquellen 78a, b, c, d, e... in einer Weise zu vollziehen, daß der aktuelle Bewegungsverlauf mit jenem früheren Bewegungsverlauf annähernd räumlich und zeitlich isomorph ist, aus dem die Zeitdaten-Sequenz Tw'(nnnn) hergeleitet wurde. Zu diesem Zweck sind das TICM 86, in das die aktuellen Zeitdaten einfließen, sowie die Speicher-Einheit 92, in der die früher erfassten Zeitdaten Tw'(nn) gespeichert sind, mit einem Kovarianz- Analysator 90 und einer Diskriminator- Logik 91 verbunden, welche die einzelne Zeitdaten verifiziert und auf Plausibilität prüft. Ungültige Zeitdaten werden gelöscht oder so interpoliert, dass kein Ausfall eines datengestützten Regelkreises auftreten kann. Analysator 90 und Diskriminator 91 suchen den Speicher 92 mit sehr hoher Frequenz fortgesetzt nach annähernd übereinstimmenden Zeitdatenmustern ab. Signifikante Datensequenzen werden an den Interpreter 93 weitergeleitet, welcher über die jeweilige Wahrscheinlichkeitsdichte und das Ausmaß der Kovarianz entscheidet. Besteht ausreichende Übereinstimmung, so errechnet der Prozessor 94 die entsprechenden Aktivierungsparameter Tempoverteilung zur Erzielung eines isomorphen Bewegungsverlaufes. Diese Daten gelangen an das Steuerungsmodul 95, wo sie in Impulse 96, 97 für das Antriebs- Bremssystem und 98, 99 umgesetzt werden. Es ist ferner von Vorteil, in diesen Prozess auch energetische Impulse für ein Lenk- und Gegenlenksystem 100, 101, 102, 103 einzubeziehen, das auf denselben beschriebenen Funktionsprinzipien aufbaut und das für die Einhaltung des ebenfalls von besagten Tw'- Zeitmustern festgelegten räumlichen Bewegungsverlaufes sorgt. Voraussetzung für eine einwandfreie Funktion einer solchen Anordnung ist die Verwendung extrem schneller Prozes- soren zur Bedienung der Teilsysteme 90, 91, 93, 94 und 95. Der aktuelle Bewegungsverlauf des autonomen Vehikels kann nur dann annähernd isomorph zum referenten Bewegungs- verlauf werden, wenn die Erkennung der signifikanten Tw'(nnnn)-Sequenzen die Registrierung und Analyse der aktuellen Tw(1,2,3...)- Sequenzen (Ist-Werte), die Errechnung der Regelparameter und die Applizierung der Energie-Impulse 96, 97 in Echtzeit erfolgen. In diesem Fall zeigt das Vehikel eine Verhaltensweise ähnlich wie ein "Servo-Regelkreis" bekannter Art. Diese Affinität wird auch durch die Tatsache bestätigt, dass durch einfaches Erhöhen oder Verringern der Basisfrequenz fn der Zeittaktquelle 85 der gesamte zeitliche Verlauf aller einzelnen Bewegungsphasen völlig synchron beschleunigt oder verlangsamt werden kann. Jedem äußeren Eingriff, der den Bewegungsverlauf zu ändern oder zu stören versucht, wird automatisch vom Antriebsmechanismus des autonomen Vehikels entgegengewirkt. Deshalb ist ein autonomer Mechanismus, der nach diesen Prinzipien arbeitet, mit einem "lebenden Organismus" vergleichbar.Da in den System-Elementen 90, 91, 93, 94 und 95 das Bestreben programmiert ist, die Analyse und Interpretation der erfaßten Zeitparameter fortgesetzt zu verbessern (z.B. nur solche Tw'(nnnn)- Zeitdaten zu erlauben, die der kürzesten und effi- zientesten Linienfolge zuzuordnen sind), existiert in einem solchen Mechanismus nicht nur ein Bestreben nach zeitlicher und motorischer Auto-Adaption, sondern auch eine "Optimierungs- Tendenz". (Dies ist auch in molekular/biologischen Strukturen von Organismen inhärent (s. auch Beschreibung zu Fig. 4a - 4f).   Das System ist auch imstande, Prioritäten zu setzen, sowie sich für Tw'-Zeitdatensequenzen zu entscheiden, die mit einer anderen Regressionskurve korrespondieren, falls z.B. eine irreguläre Bahnabweichung erkannt wird, die vom Steuerungsmodul 95 nicht mehr stabilisiert werden kann; daraufhin strebt das Vehikel einem neuen Bewegungs- verlauf und einer neuen Tempoverteilungs -Kurve (Timing) nach. Im Memory des TICM 86 können beliebige alternative Bewegungs-Szenarien in Form von Tw'- Zeitdatenmustern gespeichert sein, auf die "zugegriffen" werden kann, wenn es eine bestimmte Kursabweichung erfordert. Auf diese Weise sind Crash-Situationen bereits im Ansatzpunkt zu erkennen und können verhindert werden, indem das Vehikel in der Lage ist, in autonomer Weise entgegenzuwirken. Das System gerät nur dann außer Kontrolle ("chaotischer Zustand"), wenn keinerlei aus früher registrierten Tw-Sequenzen abgeleitetes Regressionskurven-Segment gefunden worden ist, welches mit irgendeinem Regressionskurven-Segment konvergent ist, das aus aktuell registrierten Tw-Sequenzen abgeleitet ist. Dieser Prozess wird vom Anmelder als "motorische Auto-Adaption" oder als "Auto-Emulation" bezeichnet. Um zeitlich/räumliche Zustands- veränderungen der physikalischen Umgebung aus subjektiver Sicht des autonomen Systems zu identifizieren, genügt es in den meisten Fällen nicht, externe räumliche Strukturen, Landmarken und Lichtverhältnisse mittels optischer oder foto-elektrischer Sensoren passiv abzutasten. Üblicherweise ist es auch nötig, die Höhenabweichungen mittels Neigungssensoren, Wegunebenheiten mittels Druckaufnehmer oder Beschleunigungs-Sensoren, stationäre akustische Quellen mittels Mikrofone, Gradienten mittels Magnetfeld-Sensoren; sowie Positionen mittels GPS-Empfänger abzutasten, um genügend STQ-Zeitparameter als Referenzbasis zu gewinnen. Alle diese aufgenommenen Tw(n)-Zeitdatenströme werden im Memory des TICM gespeichert. Daraus kann man folgern, dass die Lern- und Selbstorganisations-Fähigkeit eines Organismus (bzw. eines autonomen auto-adaptionsfähigen Mechanismus) proportional zur Menge aller verfügbaren Sensoren bzw. zur Anzahl aller dem Autoadaptions-prozess verfügbar gemachten STQ- Parameter zunimmt. Eine weitere wichtige Erkenntnis ist, dass es kein Timing ohne begleitende Zeitnahme (= STQ-Quantisierung) gibt. Auto-adaptive Prozesse und Mechanismen der beschriebenen Art werden für viele zukünftige Aufgaben im Bereich der Hochtechnologie, z.B. für die Entwicklung autonomer Robotersysteme, unverzichtbar sein. Ein Beispiel dafür ist folgendes: Ein Automobil, das sich im Straßenverkehr in autonomer Weise sicher und effizient fortbewegen soll, muss imstande sein, seitliche und frontale Abstände sowie fixe Geschwindigkeitsphasen einzuhalten. Mehr noch: es muss auch fähig sein, selbsttätige Überholmanöver auszuführen, und Gefahrensituationen antizipierend zu erkennen und zu vermeiden. Dies ist nur möglich, wenn der On-Board-Computer im Fahrzeug mit einer Vielzahl verschiedener Sensoren zur Erfassung vielfältiger Signalquellen gekoppelt ist, und wenn er über eine sehr schnelle und effiziente Hardware und Software verfügt, welche jene STQ-Zeitdaten, die für die Autoadaption benötigt werden, annähernd in Echtzeit verarbeiten kann. Zukünftige Typen von Mikroprozessoren könnten um eine hardwaremäßige Struktur erweitert werden, welche die beschriebenen Funktionen vollbringen. Fig. 6a zeigt die Konfiguration einer einfachen Verkörperung eines Aspekts der Erfindung, bei der die in Fig. 2a - 2c erläuterten STQ(v)-, STQ(i)- und STQ(d)-Quantisierungsmethoden zur Erkennung von räumlichen Profilen oder Strukturen angewandt werden. Im hier gezeigten Anwendungsfall soll ein Roboterarm, auf zwei benachbarte Metallsensoren 104, 105 im Abstand B installiert sind, fähig sein, das Profil des Metallstabes 106 von anderen zu unter- scheiden, während er sich mit beliebiger Geschwindigkeit an beliebigen Stäben 106, 107, 108 usw. entlang bewegt.   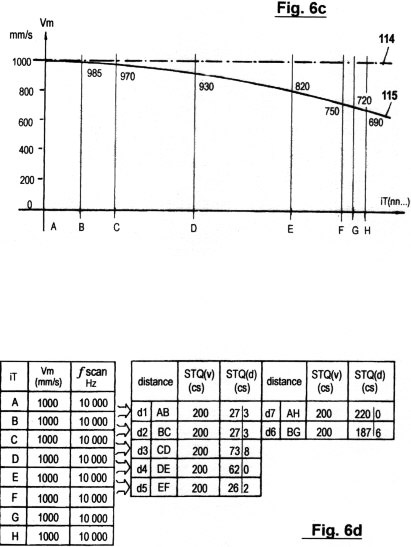Bewegt sich der Sensorkopf in der Höhe h entlang der bezeichneten Richtung, so gelangen der v- Sensor 104 (S2) und dann der w-Sensor 105 (S1) nacheinander in jenen niedrigen sensitiven Bereich, der hier als "Wahrnehmungsintensitätszone 3" bezeichnet ist. Der niedrigste Schwellwert P1 wird von der Signal-Amplitude durchbrochen, und die im Wesent- lichen aus den Elementen 81, 82, 83, 84, 85, 86, 87, 88, und 89 bestehende Aquisitions-Logic 109 (s. auch Fig. 5) beginnt mit dem Erwerb vm- modulierter STQ(i)- STQ(d)- Zeitsequenzen Tw(1,2,3...n) und Td(1,2,3...n), die im TICM-Memory (A) 110 gespeichert werden. Derselbe Zeitdatenerfassungs-Prozess wiederholt sich, wenn die Sensoren 104, 105 auf die nächsthöheren Wahrnehmungsbereichszonen 2 und 3 treffen und die Signalamplituden die in den Schwellwertdetektoren eingestellten Potentialwerte P2 und P3 durchbrechen. Um jene Metallstäbe 106, die das charakteristische Profil aufweisen, im Analysator 112 eindeutig zu identifizieren, müssen die Tw,Td-Zeitdatenströme, welche ins Memory 110 einfließen, fortgesetzt mit jenem signifikanten Tw',Td'-Zeitdatenmuster (B) 111 verglichen werden, das als "Referenzmuster" vorprogrammiert worden ist. Ungültige oder irreguläre - in der Diskriminator-Einheit 113 erkannte - Zeitdaten werden sodann gelöscht oder korrigiert. Diese Einheit ist auf die Fähigkeit programmiert, die Zuordnung und Verarbeitung der Daten automatisch zu verbessern (d.h. die Zeitdaten in auto-adaptiver Weise zu überprüfen und zu verifizieren) wie dies schon in bezug auf Fig. 5 beschrieben wurde. Wurde ein Profil als solches erkannt, so gibt der Analysator 112 ein Bestätigungssignal an eine Aktuator-Einheit des Roboters weiter, die dann einen Mechanismus in Gang bringt, der die identifizierte Metallschiene vom Boden abhebt, auf ein Laufband aufsetzt usw. Fig. 6b - e zeigen verschiedene Diagramme und Tabellen bezüglich Fig. 6a. Fig. 6b zeigt ein Sensorfeld-Diagramm des abgetasteten Metallprofils 106. Die Messung seiner Dimensionen d1....d7 resultiert ausschließlich aus STQ- Quanten, d.h. in der Zeit- domäne. Identifikation der Profile sind 3 Empfindlichkeitszonen (P1, P2 und P3) vorgesehen, die in Schwellwert-Detektoren gespeichert werden. Zu den Phasendurchgängen (iT)A, (iT)B, (iT)C, (iT)D, (iT)E, (iT)F, (iT)G und (iT)H werden digitale Präzisionszeitmesser gestartet oder gestoppt. Da die variable Zeitzählfrequenz ƒscan, mit der diese Zeitmesser zählen, automatisch an die Abtast-Geschwindigkeit vm angepasst (bzw. moduliert) wird (siehe auch Fig. 3a - g, und Fig. 5), korrelieren die tatsächlichen Dimensionen d1....d7 weitgehend mit den Tw,Td- Verstreichzeiten, die bereits im Memory 110 gespeichert sind. Wie aus der Zeichnung ersichtlich, erhält man die Distanzen AB-(d1) und BC-(d2) aus STQ(d)-Verstreich zeiten, die Distanzen CD-(d3), DE-(d4), EF-(d5) sowie BG-(d6) und AH-(d7) aus STQ(i)- Verstreichzeiten. Einmal mehr wird vom Patentanmelder bekräftigt, daß alle (iT)n... flüchtige Phasendurchgänge darstellen, und niemals "Zeitpunkte" nach klassischem physikalischem Verständnis. Fig. 6c zeigt die vm-Diagramme zweier Bewegungsverläufe der Sensoren S1 und S2 entlang des abgetasteten Metallprofils. Im einen Fall bewegt sich der Roboterarm, auf dem die beiden Sensoren montiert sind, mit einer konstanten Geschwindigkeit von 1000mm/s über dem Profil (strichpunktierte Linie 114). Im anderen Fall wird die Geschwindigkeit des Arms von 1000mm/s beim ersten Phasendurchgang A bis auf 690mm/s beim letzten Phasendurchgang H abgesenkt. Diese Absenkung ist nicht linear, sondern folgt dem Verlauf der Linie 115.   Fig. 6d zeigt eine fiktive Frequenz- und Zeitdatentabelle zu Fig. 6c bei einer gleichbleiben- den relativen Geschwindigkeit von vm=1000m/s an allen Phasendurchgängen (iT) A...H. Daraus ergibt sich eine vm-modulierte Zeitzählfrequenz ƒscan von 10 kHz während des gesamten Abtastvorganges. Da im vorliegenden Fall die STQ(v)-Verstreichzeitmessung mit einem fixen (primären) Quellen-Zeittakt von 200cs/b erfolgt, resultieren aus dem Scanning- Prozess vm-adaptierte STQ(d)-Verstreichzeiten von 273cs, 273cs, 738cs, 620cs und 262cs für die Distanzen AB, BC, CD, DE und EF sowie vm-adaptierte STQ(i)-Verstreichzeiten von 1876cs und 2200cs für die Distanzen BG und AH. Diese aus STQ(d)- und STQ(i)-Verstreich- zeiten bestehende aktuelle Tw,Td-Sequenz wird im Analysator 112 mit der referenten gespeicherten Tw',Td'-Sequenz 270cs, 270cs, 740cs, 620cs, 260cs, 1880cs, 2200cs verglichen, welche als signifikantes Zeitmuster für dieses Metallprofil dient, das bereits im Memory 111 gespeichert ist. Entscheidet der Analysator, daß "Übereinstimmung" besteht, so wird ein Bestätigungssignal an eine Aktuator-Einheit ausgegeben. Der Analysator verfügt über Komparatoren und/oder "Fuzzy-Logic"-IC's, welche die Streuungen in Grenzbereichen ignorieren (z. B. Dezimalstellen aufrunden). Abgesehen von diesen Korrekturmaßnahmen lassen sich auch Toleranzen, Plausibilitätskriterien und Zuordungskriterien softwaremäßig programmieren. Fig. 6e zeigt dieselbe Frequenz- und Zeitdatentabelle wie Fig. 6d, jedoch mit variablem Verlauf der Abtast- Geschwindigkeit(vm). Die Relativgeschwindigkeit von 1000mm/s an Phasendurchgang (iT)A nimmt auf 690mm/s beim letzten Phasendurchgang (iT)H ab. Die vm- Absenkung ist nicht linear. Entsprechend des Verlaufes des Graph 115 werden zu den Phasendurchgängen (iT)A, B, C, D, E, F, G, H die einzelnen Momentangeschwindigkeiten (vm1,2,3..) 1000; 985; 970; 930; 820; 750; 720 und 690mm/s gemessen. Die besagte vm- adaptive Modulation der Zeitzählfrequenz ƒscan produziert zu den Phasendurchgängen die Frequenzwerte 10; 9,85; 9,70; 9,30; 8,20; 7,50; 7,20 und 6,90kHz, mit denen die STQ(i)- und STQ(d)-Verstreichzeiten quantisiert werden. Da die STQ(v)-Quantisierungen ebenfalls mit einem fixen Quellen-Zeittakt von 200cs/b erfolgt, resultieren für die Distanzen AB, BC, CD, DE, EF, BG und AH dieselben Tw,Td-Verstreichzeit-Sequenzen, wie in Tabelle Fig. 6d. Daraus ist ersichtlich, dass die Erkennung des besagten Metallprofils sowohl bei linearer als auch bei nichtlinearer vm-Tempoverteilung gewährleistet ist.
		Fig. 7a - d zeigen verschiedene Sensor-Konfigurationen zur Quantisierung von STQ(v)- Verstreichzeiten bzw. zur Erfassung der Relativgeschwindigkeits-Parameter (vm). Die ersten drei Konfigurationen zeigen Sensoranordnungen für 2-dimensionale Erfassung von externen Ereignissen, Fig. 7d zeigt eine besondere Konfiguration anwendbar für beliebige drei- dimensionale Erfassung der physikalischen Umgebungen. Fig. 7a zeigt eine Sensoranordnung, bei dem eine Halterung, die S1 und S2 in Entfernung b auf gleicher Achse trägt, sich in der gekennzeichneten Richtung entlang einer willkürlichen Bahn bewegt, bzw. sich auf einer Oberfläche um ein räumliches Zentrum A in Äquidistanz zu S1 (V-Sensor) und S2 (W-Sensor) dreht. Dieses Sensor-System verfügt nur über einen Freiheitsgrad. Fig. 7b zeigt eine Sensoranordung, bei dem eine Trägerfläche, die auf gleicher Achse zwei V-Sensoren S2 und einen in Äquidistanz b zu beiden befindlichen W-Sensor S trägt, sich beliebig in einer der beiden gezeigten 180° entgegengesetzten Richtungen entlang einer willkürlichen Bahn bewegt, bzw. beliebig um einen im Raum befindlichen Punkt A dreht, der äquidistant zu beiden V-Sensoren S2 ist. Die beiden in Fig. 7a und Fig. 7b gezeigten Sensoranordnungen sind für die meisten verkehrstechnischen Robotik-Anwendungsgebiete ausreichend. Fig. 7c zeigt eine Konfiguration mit einer Anzahl gleichgearteter V-Sensoren S2, die als Segmente rund um einen zentralen W-Sensor S1 auf einer kreisförmigen Trägerfläche mit Radius b gruppiert sind. Bei dieser Konstellation kann sich die Trägerfläche in irgendeiner Richtung auf willkürlicher Bahn bewegen, oder sich beliebig um einen in irgendeinem Sensor- Abstand im Raum befindlichen Punkt drehen. Diese Sensoren-Anordnung verfügt daher über 2 Freiheitsgrade. Fig. 7d zeigt eine Sensor-Konfiguration mit einer Vielzahl von V-Sensoren S2, die als Seg- mente auf einer kugelförmigen Trägerfläche im Radius b rund um einen zentralen W-Sensor S1 gruppiert sind. Die Sensor-Anordnung kann sich zu beliebiger Position im dreidimensionalen Raum bewegen oder in beliebiger Richtung um ein festes räumliches Zentrum A mit beliebigem Abstand zu den Sensoren rotieren. Diese Konfiguration verfügt über 3 Freiheitsgrade. Die in Fig. 7c und Fig. 7d gezeigten Sensor-Anordnungen kommen in erster Linie für autonome Erkundungsroboter oder Flugobjekte in Frage, bei denen Antriebs-Impulse in beliebiger Richtung appliziert werden können (z.B. mittels Steuerungsraketen). Fig. 8a - f zeigen die Konfiguration und Funktionsprinzipien einer weiteren Verkörperung der gegenständlichen Erfindung, bei der die in Fig. 2a, b, c beschriebenen STQ-Quantifizierungs- Methoden zur Schaffung eines autonomen lernfähigen selbstorganisierenden Trainingsroboters für den Einsatz im Sport dienen; einen sogenannten "elektronischen Hasen". Dieses System besitzt autonome Antriebs-, Lenkungs- und Bremsmechanismen sowie einen Analysator, der die aktuell registrierten vm-adaptiven STQ(i)- und STQ(d)-Zeitstrommuster Tw,Td(1,2,3...) fortgesetzt mit früher registrierten vm-adaptiven STQ(i)- und STQ(d)-Zeitstrommuster Tw',Td'(1,2,3...) vergleicht, welche als Referenzmuster dienen. Es ist dadurch imstande, einen vom Benutzer vorgegebenen Bewegungsvorgang zu reproduzieren und zu optimieren; die idealen Routen und die Tempoverteilungen automatisch zu finden; Abstände und Zeiten einzuhalten; Gefahrensituationen zu erkennen und davor zu warnen; und die Eigenbewegung sowie Informationen über Geschwindigkeit, Rundenzeiten, Teilzeiten, Gesamtzeiten usw. auf einem Monitor darzustellen. Zusätzlich ist es imstande, diese Daten wahlweise optisch oder akustisch auszugeben. ω, are obtained from these vm-adaptive STQ(i) elapse time measurements. It would nevertheless be advantageous to acquire also STQ(d) quanta, which can serve to verify the recorded time data stream Tω .   Fig. 8a zeigt einen derartigen Trainingsroboter 116 vor einem Skilangläufer 117. Das dar- gestellte Roboter-Vehikel verfügt über ein Kufen-Fahrgestell, das die Fortbewegung schneebedecktem Boden ermöglicht. Um imstande zu sein, einem menschlichen Skifahrer entlang einer Langlaufspur zu folgen, hat es entsprechend manövrierfähig zu sein. Es muss auch fähig sein, eine Langlaufloipe selbsttätig zu spuren, wenn die alte Spur vom Schnee zugeweht wurde und daher nicht mehr sichtbar ist. Der Trainingsroboter ist speziell auch als Hilfsmittel für blinde Skiläufer geeignet. Das autonome Vehikel erkennt skiläuferische Kriterien für blinde Skilangläufer und ruft Hinweise, Berichte und Warnungen mit Hilfe von Sprachsynthese. Dies befreit den Anwender vom Gefühl, auf Hilfe angewiesen zu sein, und macht ihm mehr Freude. Das Robotervehikel 116 verfügt über eine hohe Anzahl von Sensoren und elektronischen Einheiten, wie sie in Fig. 5 beschrieben wurden. Es vollbringt dieselben darin aufgezeigten Auto-Emolutions-, Auto-Adaptions- und Auto-Optimierungs-Prozesse, wobei häufig verschiedene Aufgaben gleichzeitig durchgeführt werden. Es bezieht vm- adaptierte STQ(i)- und STQ(d)-Verstreichzeitmuster aus einer Vielzahl von Sensoren, vergleicht diese Muster mit den entsprechenden Referenzzeitmustern, wählt die signifikanten Zeitdaten aus und analysiert und errechnet Parameter für die diskreten Energie-Impulse zur Steuerung der Antriebs-, Brems- und Lenkmechanismen. Im folgenden Teil werden die wesentlichsten Komponenten des Systems unter Einbeziehung von drei spezifischen Typen von Sensoren (optische S., Magnetfeld- und GPS-Positions- Sensoren) behandelt. 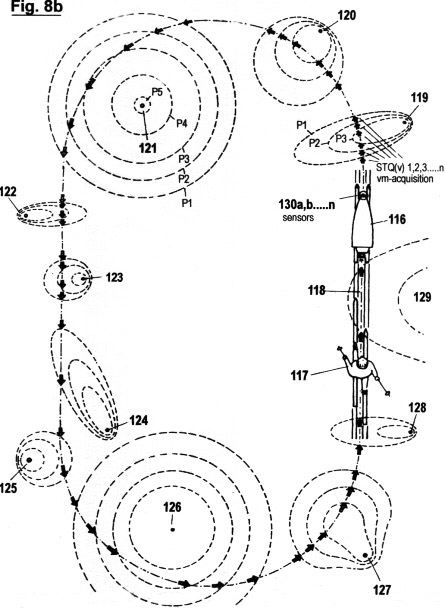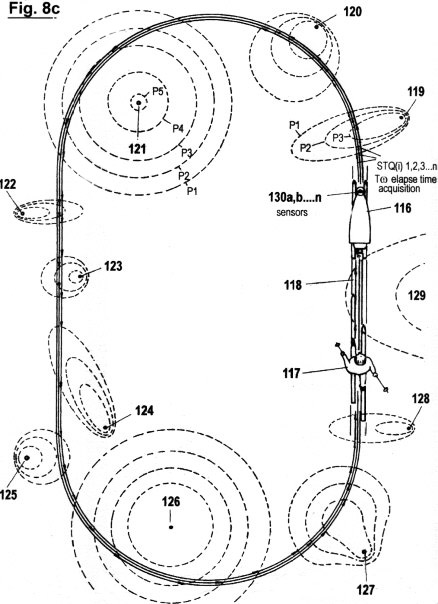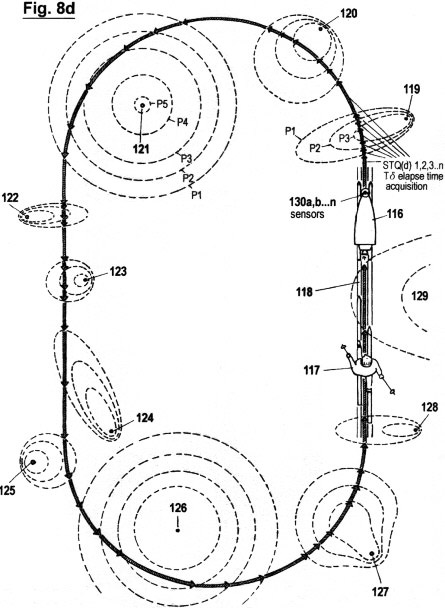Fig. 8b - d zeigen die Registrierung von STQ(v)-, STQ(i)- und STQ(d)-Verstreichzeiten (passend zu Fig. 8a) bei Verwendung optischer oder akustischer Sensoren. Die fundamenta- len Funktionsprinzipien sind zum größten Teil bereits in den Beschreibungen zu Fig. 2a, b, c und Fig. 5 enthalten. In besagten Zeichnungen bewegt sich der Trainingsroboter ("der elektronische Hase") 116 mit variabler Geschwindigkeit vor einem Skilangläufer 117 in der Loipe 118. Entlang der Spur befinden sich in willkürlicher Anordnung optische oder akustische Signalquellen 119, 120, 121, 122, 123, 124, 125, 126, 127, 128 und 129, die von ent- sprechenden Sensoren 130a, b,...n wahrgenommen werden. Bei jedem Phasendurchgang zu den Schwellwertbereichen P1, P2, P3, P4, P5 usw. werden die besagten STQ(v)-, STQ(i)- und STQ(d)-Verstreichzeiten erfasst. Sie ergeben das aktuelle vm-adaptive Tw,Td(1,2...n)- Zeitdatenmuster, das im TICM gespeichert wird. Für die prinzipielle Funktionsweise ist es nicht von wesentlicher Bedeutung, ob die Signalquellen dort stationär angeordnet sind (z.B. könnten sie Scheinwerfer sein, welche die Piste für abendliche Events beleuchten). "Signalquellen" können auch aus wechselnder Helligkeit bei Tageslicht oder aus Kontrast- und Farbunterschieden nahe Bäumen, Masten, Gebäuden, Abhängen oder signifikanten Landmarken resultieren. Scheinwerfer könnten sogar am Schulungs-Roboter selbst installiert werden, wobei die optosensorische Erfassung des reflektierten Lichts und die Evaluierung der Licht-Strukturen der räumlichen Umgebungen zur Erkennung der Eigenbewegung genutzt werden kann. Die gleiche Anordung wäre auch mit Ultraschallgeber und -sensoren machbar. Akustische Signalquellen können anderseits ebenso natürlichen Ursprunges sein, wie etwa das Rauschen eines Baches neben der Loipe, oder ein Wasserfall usw. Generell kann jedwede flüchtige Kombination von Licht und Schatten oder irgendeine Geräuschquelle signifikant für die Erkennung eines bestimmten Objekts sein. Die Bestimmung der individuellen Identität eben dieses Objekts geschieht durch Vergleich von vm-adaptiv registrierten STQ(i)- und STQ(d)-Verstreichzeit-Mustern, die für jedes einzelne Objekt stehen. Um die Beschreibung und Veranschaulichung zu vereinfachen, wird in Fig. 8b von der Annahme ausgegangen, dass die Signalquellen 119...129 fix installierte Leuchten (entlang der vom Roboter befahrenen Route) sind, welche die Benutzung der Loipe auch bei Dämmerung oder Dunkelheit ermöglichen. In Entsprechung zum primären Zweck der Anwen- dung eines solchen Roboters fährt der Trainingsroboter 116 präzise hinter dem Skilangläufer 117 in dessen Spur her, wobei alle STQ-Zeitdaten vm-adaptiv erfasst und in dessen TICM- Memory (s. auch Fig. 5) gespeichert werden. Die Entfernung zwischen Roboter und Anwender wird durch einen Entfernungs-Sensor exakt geregelt.Um aber die Antriebs-, Brems- und Lenksysteme des Robotervehikels überhaupt in Gang bringen zu können, müssten vor der Tour STQ-Zeitdaten in das TICM geladen werden, die als Referenzdaten dienen könnten. Daher werden im ersten Schritt die primär erfassten Zeitdaten in den TICM- Referenz-Datenspeicher übernommen; d.h. aus Tw,Td(1,2,3...) werden im ersten Schritt Tw',Td'(1,2,3...). In weiteren Schritten wird das Nachfahren hinter dem Läufer mehrmals mit wechselnder Geschwindigkeit und Spurverteilung wiederholt - sodass der Roboter mehr über den Skiläufer "lernt" - worauf immer mehr kovariante Tw',Td'-Zeitdatenmuster in das Referenz-Datenmemory einströmen, auf welche die Diskriminator- und Analysatoreinheit des Roboters zugreifen kann (s. gleichfalls Fig. 5). Nunmehr setzt das Interpretations- und Optimierungsprogramm ein, welches nur "authentische" Tw',Td'- Zeitdaten herausfiltert, die als signifikant für die beste und effizienteste Linie scheinen, und welches gleichzeitig die als "irrelevant" erkannten Zeitdaten eliminiert. Dies kommt einem "Lernprozess" gleich, den das Robotervehikel zu absolvieren hat, bis es schließlich "autonom skilaufen" kann, d.h. relativ frei, und nach selbsttätig angeeigneten Mustern und Selbstentscheidungs-Kriterien; ohne irgendeine Fernsteuerung oder Regelung durch einen vorprogrammierten Algorithmus. In dieser Phase fungiert der Trainings-Roboter als "Trainer" oder "Pilot", der die Aufgabe hat, dem Benutzer zu helfen, ideale Geschwindigkeitsverläufe, die beste Spur und optimales Timing zu finden. Die optimale Information, die dem Anwender übermittelt wird, besteht immer nur aus jener, die vom Roboter selber "erlernt" worden ist. Der Trainingsroboter fährt auch bei seiner "praktischen Arbeit" (d.h. während er dem Anwender behilflich ist) fort, sich weiter zu verbessern, und seine im TICM gespeicherten STQ-Referenzdaten fortgesetzt zu optimieren und zu ergänzen. Die Fähigkeit, Bewegungs- verläufe oder externe Signalverläufe und Objekte zu identifizieren und zu erkennen, ist ausbaufähig. Sie hängt von der Menge und Vielfalt der benutzten Sensoren und von der Speicherkapazität des TICM ab. Somit ist es möglich, das Robotervehikel zu veranlassen, Gefahrenszenarien zu erkennen und davor akustisch oder optisch zu warnen, sowie Abstände und Zeiten genauer einzuhalten. Im vorliegenden Anwendungsfall führt das Vehikel das automatische Spuren und Nachlaufen entlang einer Loipe sogar dann durch, wenn die Fährte zuvor von einem Schneesturm verblasen wurde und nicht mehr sichtbar ist. Außerdem hat das Robotervehikel einen Monitor, auf dem die Eigenbewegung in bezug zur räumlichen Umgebung visualisiert werden kann, und es verfügt über elektronische Maßnahmen, um Geschwindigkeiten, Rundenzeiten, Teilzeiten, Gesamtzeiten oder andere relevante Daten in optischer oder akustischer Weise auszugeben. Eine wichtige Eigenschaft des hier gezeigten Roboters besteht auch darin, dass die Geschwindigkeitsphasen in allen Streckenabschnitten durch einfache Veränderung (Erhöhung oder Verminderung) des Quellen-Zeittakts synchron beschleunigt oder verlangsamt werden kann. Diese Eigenschaft ist beispielsweise erforderlich, um das Tempo des Trainingsroboters in allen Abschnitten entsprechend der körperlichen Fitness des Anwenders anzupassen. Dies kann manuell per Fernbedienung oder automatisch - z.B. mittels Puls- oder Blutdruck-Datentransponder - geschehen.   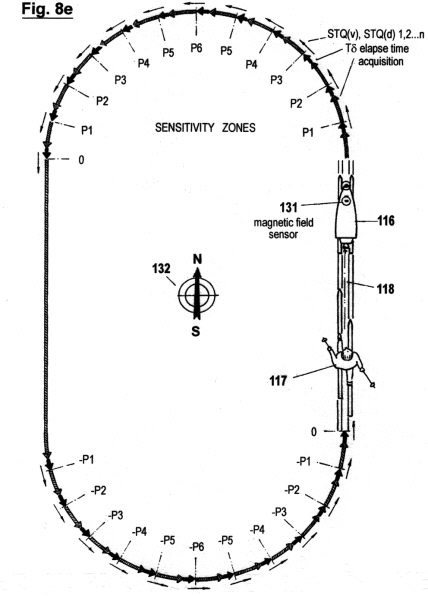Fig. 8e zeigt die Erfassung von STQ(v)- und STQ(d)-Verstreichzeiten für den Roboter in Fig. 8a, für den Fall, dass Magnetfeld-Sensoren installiert sind. Als Signalquelle wird hierbei das Erdmagnetfeld angenommen. Im gezeigten Beispiel, wo die Spur einen geschlossenen Kreis bzw. eine Schleife bildet, ist die Quantisierung von STQ(i)-Verstreichzeiten uneffizient und daher nicht vorgesehen. Im bezeichneten Bild bewegt sich der Trainingsroboter ("Hase") 116 autonom mit variabler Geschwindigkeit vor dem Ski-Langläufer 117 entlang der Loipe 118. Dabei ergeben sich entlang der Spur unterschiedliche Fahrzeug-Positionen mit variablen Gradienten in bezug zum Erdmagnetfeld 132. Die Magnitude dieser Gradienten wird vom Magnetfeld-Sensor 131 erfasst. Im gezeigten Fall hätte die Magnitude einen sinusförmigen Verlauf. Bei jedem Phasendurchgang zu den Schwellwertzonen P1, P2, P3, P4, P5, P6 usw. werden die besagten STQ(v)- und STQ(d)- Verstreichzeiten adaptiv erfasst und ergeben das aktuelle Td-Zeitdatenmuster, das im TICM gespeichert wird. Die zusätzliche Quantisie- rung von STQ-Verstreichzeiten aus Magnetfeld-Gradienten erleichtert die Ortung kovarianter Tw',Td'-Zeitmuster, die im Referenzdaten-Speicher enthalten sind. Infolgedessen verbessert sich die Autoadaptions- und Erkennungsfähigkeit des Roboter-Vehikels. Je mehr Sensoren in den Autoadaptionsprozess beteiligt sind, desto "autonomer" wird der beschriebene Mechanis- mus (s. auch Fig. 5). In dieser Weise kann ein auf biologisch/chemischen Strukturen basierender selbstorganisierender autonomer Organismus, wie in Fig. 4a - f beschrieben wurde, geschaffen werden.   Fig. 8f zeigt die Erfassung kreisförmiger Positionsfelder mittels GPS-Sensoren. Diese Maß- nahme dient (zusätzlich zu jenen in Fig. 8b - e) zur weiteren Verbesserung der zeitlichen und motorischen Auto-Adaption, und zu einem präziseren Autokovarianz-Verhalten und Bewegungs-Nachvollzug. Vorbedingung für eine exakte Funktion ist ein GPS ("global positioning system") von hoher Qualität, die mit äußerst geringen Abweichungen arbeitet. Da in diesem Fall ein rechteckiger Signalverlauf empfangen wird und daher keine Unter- teilung in unterschiedliche Empfindlichkeits-Zonen möglich ist, können nur STQ(v)- und STQ(i)-Verstreichzeiten, nicht jedoch STQ(d)-Verstreichzeiten quantisiert werden (welche - wie gezeigt - zwischen niedrigeren zu höheren Phasendurchgängen und vice versa gemessen werden). In Fig. 8f bewegt sich der Trainingsroboter ("Hase") 116 mit variabler Geschwindigkeit vor dem Skilangläufer 117 entlang der Loipe 118, wobei sich entlang der Spur kreisförmige GPS-Positionsfelder 134a, b...n ergeben, die vom GPS-Sensor 133 mit hoher Messgenauigkeit in reproduzierbarer Weise wahrgenommen werden. Die Radien der Positionsfelder sowie die Trennschärfe zwischen benachbarten Feldern sind justierbar. Bei jeder Detektierung eines neuen Positionsfeldes wird ein Triggersignal an die STQ- Aquisitionseinheit ausgegeben, welches die Registrierung der STQ(v)- und STQ(i)-Verstreich- zeiten veranlaßt, die dann als aktuelle vm-adaptive Zeitdatensequenzen Tw(1,2,3....) im TICM gespeichert werden. Die Fähigkeit des Roboters zur Optimierung der Auto-Adaption kann gesteigert werden, indem die Anzahl der detektierten Positions-Felder gezählt und verglichen wird, oder indem man den Zeitdaten bei jeder Querung eines Positionsfeldes einen spezifischen Datencode zuordnet. Fig. 9 ist eine allgemeine schematische Darstellung, und zeigt, wie Zeitdatenströme produziert werden. Jede Amplituden-Querung von Empfindlichkeitszonen oder Schwellwert- potentialen in redundanzarmen autonomen selbstorganisierten Systemen (wie z.B. Organismen oder mechanistische Robotersysteme) führt zur Quantisierung von Verstreich- zeiten, wenn diese über entsprechende Sensoren (oder Rezeptoren) zur Wahrnehmung der externen physikalischen Umgebung verfügen. Diese Basis-Technologie, wie sie im Bild gezeigt wird, behauptet universale Gültigkeit und Anwendbarkeit. Die Darstellung zeigt ein sehr vereinfachtes Schema, das auch vom Nichtexperten klar verstanden wird.

1) Die primäre Aufgabe jedes Organismus (einschließlich autonomer selbstorganisierender     Roboter) besteht in der "Erkundung" seiner Umgebung, um festzustellen, ob zeitlich/räumliche    Variation zwischen dem physikalischen Eigenzustand und dem Zustand seiner Umgebung     besteht. Dazu dient eine Vielfalt unterschiedlicher Sensoren oder Rezeptoren 135a, b....n usw. 2) Nur wenn eine solche Variation tatsächlich existiert, werden die mit 137a, b...n bezeichneten     aktuellen STQ-Verstreichzeiten Tw(1,2,...n ) oder Td(1,2...n)abgeleitet. Die Zeitzählfrequenz zu     deren Messung ist abhängig von aktuell erfassten STQ(v)- Quanten Tv(1,2,3...n); 136a, b,c ...n     welche die Parameter für die zeitlich/räumlichen Abweichungen vm(1,2...n) zwischen Sensoren     135a,b,...nund externen Quellen darstellen. Diese Abweichungen sind mit den "relativen     Geschwindigkeiten" vm(1,2..n) ident. Anmerkung: vm(1,2...n ) werden immer mit einer     invarianten Zeitzählfrequenz f als Absolut-Zeitbasis (Quellen-Zeittakt) erfasst. 3) Die aktuellen Verstreichzeiten Tw(1,2...n) oder Td(1,2 ...n) fließen sozusagen in "Informations-     Töpfe" (Zeitdatenspeicher) 138 und bilden dort STQ-Verstreichzeitmuster Tw'(1,2... .n) oder     Td'(1,2... .n), die als Referenz-Muster dienen. Findet der Organismus Sub-Sequenzen solcher     Tw',Td'-Muster, die in irgendeiner Kombination kovariant sind mit einem aktuell registrierten     Tw,Td -Muster, so interpretiert der Organismus diese Kombinationen als "isomorphes Muster",     das signifikant ist für die Bestimmung des tatsächlich wahrgenommenen Ereignismusters (d.h.     "was eigentlich ist"). Auf diese Weise wird das aktuelle Ereignis (resultierend aus den zeitlich/     räumlichen Zustandsveränderungen zwischen Sensoren und externen Signal-Quellen)"erkannt". 4) Ein Organismus verfügt über "Aktuatoren", die eine auf sich selbst bezogene aktuelle     Veränderung eines zeitlich/räumlichen Zustands (z.B. seine eigene Bewegung) so beeinflussen,     das Muster dieser Veränderung weitgehend kovariant ist mit einem früher registrierten Muster     einer zeitlich/räumlichen Zustandsveränderung (genauer gesagt: diesem "nacheifert"). Da     außerdem bei der Speicherung neuer Tw,Td-Sequenzen immer wieder das kürzeste und     effizienteste Zeitmuster Priorität hat, versucht der Organismus fortgesetzt, besagte     zeitlich/räumlichen Zustandsveränderungen zu optimieren. Beide Prozesse resultieren     ausschließlich aus dem Vergleich von quantisierten STQ-Verstreichzeiten und aus der     Erkennung von isomorphen Zeitdatenmustern (s. dazu auch Fig. 5), und werden als "Auto-     Emulation" und "Auto-Optimierung" oder aber auch als "Bestreben nach Autokovarianz"     bezeichnet. 5) Eine essentielle Konsequenz dieser Betrachtungen besteht darin, daß in allen Organismen der     beschriebenen Art eine inhärente teleologische Tendenz zu fortgesetzter Auto-Adaptation     und Auto-Optimierung besteht. Dies ruft die Fähigkeit zur Selbstorganisation hervor. 6) Wie aus Fig. 10 eindeutig zu sehen ist, hängen sowohl "Zeit" als auch "Geschwindigkeit" von     der Existenz entsprechender Sensorik zu deren Wahrnehmung ab. Genau genommen fließen     alle Zeitdaten und Informationen aus der "Gegenwart" (dem Ursprung der Erfassung) in     Richtung "Vergangenheit" (der nachweisbaren Existenz). Tatsächlich werden Zeit und     Geschwindigkeit nicht als Kontinuum "erfühlt", sondern in Form von Quanten. Um beide     physikalischen Größen als kontinuierlichen Verlauf zu empfinden, erfordert es in einem     Organismus enorme Autoadaptions- und Autoemulations-Fähigkeit. Es kann gesagt werden,     dass die angeführten fundamentalen Prinzipien nicht nur für Robotik und biologische Einheiten     gültig sind, sondern auch für molekulare, atomare und subatomare Strukturen.     Auch bei diesen hat es sich um "zeitempfindende Organismen" zu handeln, ansonsten hätten     sie keine Basis, um zu existieren. Fazit: Es gibt weder Zeit noch Raum ohne irgendeine     andere physikalische Größe ohne subjektive Empfindungsfähigkeit dafür. Objektiv gesehen     existiert im Universum ausschließlich Sensorium mit unterschiedlichen Empfindlichkeits-     bereichen; und daraus resultiert lokale subjektive Zeitempfindung und ein generelles     universelles Bestreben nach Autoadaption, Auto-optimierung und Auto-Emulation. Dies ist     ein fundamentales teleologisches Ordnungsprinzip.

Der Anmelder fasst einige daraus resultierende neue wissenschaftliche Erkenntnisse und Theorien zusammen und postuliert wie folgt:

1) Die hierin beschriebene erfindungsgemäße Methode ist universell anwendbar und zeigt     die äußerste (ultimative) Höhe des erreichbaren Stands der Technik auf. 2) Zeitdiskrete Quantisierungsmethoden, in deren Zusammenhang eine empfangene     Signalamplitude zu vorbestimmten Zeitpunkten abgetastet und digitalisiert wird, erweisen sich     erweisen sich als zu schwach, um daraus hocheffiziente autonome Selbstorganisations-     Prozesse zu generieren. 3) In redundanzfreien autonomen selbstorganisierenden Systemen gibt es keine "Zeitpunkte" und     keinen Determinismus. In diesen Systemen werden Verstreichzeiten quantisiert, die aus der     zeitlich/räumlichen Zustandsveränderung zwischen Sensoren und externen Quellen herleiten. 4) Jedes derartige System verfügt über seinen eigenen Zeittaktgeber und produziert seine eigene     Zeit. Die Zeitzählfrequenz zur Quantisierung von Verstreichzeiten wird in auto-adaptiver Weise     stets an jene relative Geschwindigkeit vm angepasst, mit der Zustandsveränderungen auftreten.     Die Zeiterfassung hat in jedem Fall Quantennatur, d.h. sie hat die Eigenschaften einer diskreten     "Zählung", egal ob die Erfassung analog, digital oder in sonstiger Weise erfolgt. Außerdem ist     die Zeiterfassung subjektiv/passiv, d.h. die Zeitquanten werden "erfühlt" und nicht im     konventionellen physikalischen Sinne "objektiv gemessen". 5) Um imstande zu sein, in autonomen selbstorganisierenden Systemen Verstreichzeiten     quantisieren zu können, müssen die einzelnen Sensoren oder Rezeptoren über unterschiedliche     Grade (Zonen) von Wahrnehmungsbereichen (oder Schwellwerten) verfügen. 6) Um den Unterschied zwischen "Synchronität" (nach konventionellem Verständnis)     und "Auto-Adaption" klarzustellen, sei wie folgt definiert:        a) Parallele Synchronität (kurz: "Synchronität"): d.h. die zeitlichen Änderungen der            physikalischen Zustände verschiedener Systeme verlaufen zur gleichen Zeit kovariant.        b) Autonome Adaption (kurz: "Auto-Adaption"): d.h. die zeitlichen Änderungen des            physikalischen Zustandes des gleichen Systems verlaufen zu verschiedenen Zeiten            kovariant. 7) In allen redundanzfreien autonomen Systemen erhöht sich die Fähigkeit zur Selbstorganisation     mit der Menge der dem autonomen Anpassungs- und Optimierungsprozess verfügbar     gemachten Verstreichzeit-Parameter sowie mit der Anzahl und der Vielfalt der beteiligten     Sensoren bzw. Rezeptoren. 8) Bei "Synchronität" (Definition s. 6a oben) geht im Idealfall die Anzahl quantisierter     Verstreichzeitparameter gegen Null, in 6b aber gegen Maximum (wobei außerdem o.g. Pkt. 7     gilt! ). Daher kann davon ausgegangen werden, dass allen autonomen Systemen der genannten     Art ein Bestreben nach fortgesetzter Auto- adaption, Auto-optimierung und "motorischer     Nacheiferung" innewohnt. Dieses Bestreben hat eine Affinität zum biologischen Begriff     "Lebenskraft". 9) In autonomen selbstorganisierenden Systemen existiert kein "Timing" (d.h. zeitlich/     räumliche Koordination einer Bewegung) ohne den Vergleich aktuell erworbener Verstreichzeit-     muster mit früher erworbenen Verstreichzeitmustern. Kurz gesagt: es gibt kein "Timing"     ohne begleitende "Zeitnahme". 10) Auto-Adaptions-Satz von Erich Bieramperl:    Jede aktuelle nicht-chaotische Zustandsveränderung (A) eines autonomen Systems (X) mit dem     variablen dynamischen Verlauf vm(1,2,3..n) unterliegt einer aktuellen Folge von Verstreichzeiten     TW(1,2,3 ..n) sowie einer kovarianten Folge von Versteichzeiten TW'(1,2,3..n) aus einer zeitlich     versetzten Zustandsveränderung (A') oder aus einer Kombination unterschiedlich zeitlich ver-     setzter Zustandsveränderungen (A1')(A2')..(An'), wonach (A) mit (A') oder (A) mit (A1)(A2)...(An')     annähernd isomorph ist.      wobei:TW = vm-adaptiv erfasste aktuelle STQ(i)- oder STQ(d)-Verstreichzeit Tw oder Td         und:TW' = vm-adaptiv erfasste kovariante STQ(i)- oder STQ(d)-Verstreichzeit Tw oder Td     Weitere wissenschaftliche Konsequenzen sind folgende: 11) Jede vorsätzliche Festlegung eines bestimmten Zeitpunktes für eine beabsichtigte Handlung -      ein sogenannter "Willensakt" eines autonomen Organismus - resultiert seinerseits aus      fortgesetzter autonomer Adaption der beschriebenen Art und ist daher in deterministischer      Weise nicht realisierbar. 12) Aus der Fähigkeit eines autonomen Systems, zu aktuell erfassten Verstreichzeitmustern      passende früher erfasste Verstreichzeitmuster zu finden - und zu versuchen ihnen nachzueifern     - resultieren nicht nur Auto-Adaption, Auto-Optimierung, Selbstorganisation sowie die      Erkennung der physikalischen Umgebung und der eigenen Bewegung; sondern letztlich auch     Bewegungskoordination, Intelligenz und bewusstes Handeln. 13) Auto-adaptive, auto-optimierende und selbstorganisierende Prozesse der beschriebenen Art      haben universellen Anspruch; und zwar nicht nur auf mechanistische Systeme, Roboter,      Automaten und biologisch/chemische Organismen, sondern auch auf molekulare und atomare      Strukturen. Alle autonomen selbstorganisierenen Systeme enthalten Information in Form      von Daten in der Zeitdomäne.      Da in solchen Systemen Zeit "subjektiv empfunden" und nicht "objektiv gemessen"      wird (s. Satz 3), folgt weiters: 14) Alle zeitabhängigen physikalischen Größen werden im Universum "subjektiv empfunden". Gibt      es für Zeit und Geschwindigkeit kein entsprechendes Sensorium, so existiert auch in objektiver      Weise keine "Zeit". Beispiel: In "schwarzen Löchern" existiert deshalb keine "Zeit", weil es kein      Sensorium dafür gibt. Das atomare und subatomare Sensorium ist in diesem Fall quasi "tot". 15) Jede physikalische Zustandsveränderung, der kein auto-adaptiver Prozess zugrunde liegt,       verläuft zunehmend chaotisch, woraus folgt, dass die beschriebene Tendenz zu Auto-Adaption       im Universum der Tendenz zu Entropie und Chaos (s. zweiter Hauptsatz der Thermodynamik!)       entgegen wirkt. 16) Wenn vm zu hoch und STQ(v) zu kurz ist um gemessen (besser: "empfunden") zu werden, so       kann daraus weder ein Auto-Adaptionsprozess (da ja auch keine Verstreichzeiten ableitbar       sind) noch ein Selbstorganisationsprozess resultieren. Daher ist z. B. die Lichtgeschwindigkeit       c aus jenem Grund eine ultimative Größe, weil sie das kürzeste STQ(v)- Quantum impliziert,       das von atomaren Strukturen "wahrgenommen" werden kann. 17) Besteht absolute physikalische Invarianz zwischen dem Sensorium autonomer Systeme und      seiner Umgebung, so können ebenfalls keine STQ-Quanten abgeleitet werden. Dies ist die      Erklärung dafür, warum beispielsweise der absolute Nullpunkt (-273,15°C) eine ultimative      physikalische Größe ist. In diesem Fall ist das atomare und subatomare Sensorium nicht      imstande, eine niedrigere Temperatur zu erkennen, weil mangels STQ-Quanten kein      Autoadaptions-Prozess mehr stattfinden kann. 18) Wie schon erwähnt, verfügen auch atomare und subatomare Strukturen über sensorische und      zeitquantisierende Eigenschaften. Ihre Beschreibung ist aus Sicht der Quantentheorie      unzureichend. Gibt es keine Messung oder Beobachtung eines Ereignisses, so existiert weder      "Zeit" noch "Geschwindigkeit" (s. auch 13). Quanten-Phänomene, wie sie beim bekannten      Doppelspalt-Experiment oder beim SCULLY-Experiment auftreten ("Quanten-      Unbestimmtheiten") sind somit auf diese Weise erklärbar. 19) Elektromagnetische Kräfte, Graviation, starke und schwache Wechselwirkungen (Kernkräfte),      sogenannte "Autokatalyse" (KAUFFMAN) , "synergetische Effekte" (H. HAKEN) oder andere      Phänomene resultieren aus der Existenz von zeit-quantisierendem Sensorium, Auto-Adaption       und Auto-Emulation. Diese Eigenschaften können als inhärentes teleologisches Ordungsprinzip      im Universum betrachtet werden (S. 8). 20) Die Fähigkeit, Zeit und Geschwindigkeit als Kontinuum und nicht als endlose Serie einzelner       Verstreichzeiten zu empfinden, erwächst seinerseits aus fortgesetzten Autoadaptions- und       Selbstorganisationsprozessen. Je höher die "Intelligenz" eines autonomen Systems als       Ergebnis solcher Prozesse, desto ausgeprägter sein subjektives Zeitempfinden und seine       Fähigkeit zur Antizipation. Folgende Konsequenzen ergeben sich daraus für Metamathematik, Aussagelogik, Erkenntnistheorie und Philosophie:

1) Da es keine "Zeitpunkte" im deterministischen Sinne gibt, kann weder ein Zustand eines     Systems zu einem "Zeitpunkt" festgestellt werden, noch können "Zeitpunkte" für künftige     Zustände festgelegt werden. Es existiert kein Determinismus irgendeiner Art. Da sowohl     die klassische Physik als auch die Quantentheorie auf der Vorbedingung basieren, dass ein     System zu einem bestimmten "Zeitpunkt" in einem bestimmten Zustand befindlich ist (im     ersten Fall als Punkte des Phasenraums, im zweiten Fall als Wahrscheinlichkeitsverteilungen     im Phasenraum) können beide Theorien nicht völlig widerspruchsfrei frei sein. (s. auch     THOMAS BREUER/ 1997) 2) Nach WIGNER (1961) müsste eine absolut universell gültige Theorie imstande sein, auch     das Zustandekommen menschlichen Bewusstseins zu beschreiben. Dazu vermag die gezeigte     Autoadaptionstheorie imstande zu sein; die Quantentheorie hingegen nicht. (Wigner postulierte,     dass komplexe Quantenmechanik nur dort eine brauchbare Beschreibung der physikalischen     Realität liefert, wo es kein "subjektives Empfinden" gibt. Der Anmelder vertritt den Standpunkt,     dass es subjektives Empfinden auch in atomaren und subatomaren Strukturen gibt.) 3) Verstreichzeitreihen wie TW und TW' sind als Ketten in einem axiomatischen formalen System     betrachtbar; wenngleich es sich dabei um ein "System in der Zeitdomäne handelt und nicht um     ein arithmetisches System im Verständnis der klassischen Zahlentheorie. Tatsächlich weist     das besagte formale System mindestens ein Axiom auf und leitet durch die Anwendung eines     bestimmten Algorithmus fortgesetzt Zahlenketten ab. Nach TURING kann ein axiomatisches     zahlentheoretisches System auch durch eine mechanische Prozedur gegeben sein, welche     Formeln und Algorithmen "produziert ".Aus diesem Grund sind daher die bekannten Logik-     Theoreme von GOEDEL, TARSKI oder HENKIN auf ein solches Modell durchaus anwendbar.     GOEDEL's Unvollständigkeitssatz zeigt, dass in jedem reichhaltigen zahlentheoretischen     Modell widerspruchsfreie Formulierungen enthalten sind, die mit den Regeln desselben Modells     nicht bewiesen werden können und demnach unentscheidbar sind. Dies gilt auch für meta-     theoretische Modelle und für meta-meta-theoretische Modelle usw. Beispielsweise ist eine     selbstbezügliche meta-theoretische Aussage nach Art der Gödel-Formulierung ~ICH BIN     BEWEISBAR weder beweisbar noch widerlegbar. Ein Entscheidungsverfahren für diese     Aussage führt zu einem unendlichen Regress. TARSKI zeigte, dass auch ein Entscheidungs-     verfahren für zahlentheoretische "Wahrheit" unmöglich ist und in einem unendlichen Regress     endet. Somit ist also eine selbstbezügliche Aussage der Art ~ICH BIN BEWEISBAR "wahr",     nicht jedoch "beweisbar".     Daraus folgt, dass "Beweisbarkeit" ein schwächerer Begriff ist als "Wahrheit". HENKIN     zeigte, dass es Aussagen gibt, die ihre eigene Beweisbarkeit und "Produzierbarkeit" in einem     spezifischen zahlentheoretischen Modell behaupten und demnach unbezweifelbar "wahr" sind     [5]. Eine Henkin's Theorem entsprechende selbstbezügliche Aussage würde etwa so lauten:     >es existiert ein zahlentheoretisches Modell, in dem ich beweisbar bin< Ketten von     quantisierten Verstreichzeiten wie TW und TW' nähern sich dem Geltungsbereich von HENKIN's     Theorem. Würde man Henkin's Logik darauf anzuwenden, so lautet ihre Aussage etwa: >ich     werde entstehen, um bewiesen zu werden<. TW und TW' sind demnach Ketten oder Aussagen,     die in einem spezifischen formalen Modell produziert werden, das sein eigenes Entscheidungs-     verfahren auf Wahrheit, Widerspruchsfreiheit, Vollständigkeit und Beweisbarkeit durch     fortgesetzte Selbst-Generierung veranlasst (s. dazu auch Beschreibung zu Fig.10).     Im Gegensatz zu selbstbezüglichen Ketten oder Sätzen des Gödel- oder Henkin-Typs       behaupten Verstreichzeitketten nie, zu einem gegenwärtigen Zeitpunkt "wahr",     widerspruchsfrei", "vollständig" oder "beweisbar" zu sein, da jenes "zahlentheoretische     Modell", in dem sie produziert werden, gar keine "Zeitpunkte" kennt. Dieses Modell verbietet     auch übergeordnete Semantiken oder Meta-Theorien oder Meta-Meta-Theorien usw. Es ist klar     ersichtlich, dass jedes formale System, jede Meta-Theorie, jede Meta-Meta-Theorie und jede     Semantik, in der Axiome oder Ketten oder Sätze irgendeiner Art formuliert werden, das     Ergebnis fortgesetzter autonomer Adaption ist (die wiederum auf der Quantisierung von     Verstreichzeiten basiert) und somit eine Ableitung aus dem beschriebenen Modell ist. 4) Die Erkenntnis, dass ein spezifisches formales System mit absolutem universellen Anspruch     existiert, aus dem alles Seiende hervorgegangen ist und dem alle anderen Systeme     unterzuordnen sind, ist nicht neu. Bereits im frühen Altertum (viele Jahre vor PLATO und     ARISTOTELES) ließen die Hebräischen Schriften (2. Moses 3-14) den "Quell aller Logik" von     sich selbst sagen: "JHWH" (gesprochen: Jahwe oder Jehova), was soviel bedeutet wie: >Ich     werde mich als seiend erweisen<. Dieser Satz behauptet also sein eigenes Entscheidungs-     verfahren auf Beweisbarkeit, Wahrheit, Vollständigkeit und Widerspruchsfreiheit in einem     spezifischen formalen System, das er veranlasst, zu "werden". 5) Es gibt keine "Erkennung" ohne "Wiedererkennung".

           you are the visitor Nr :